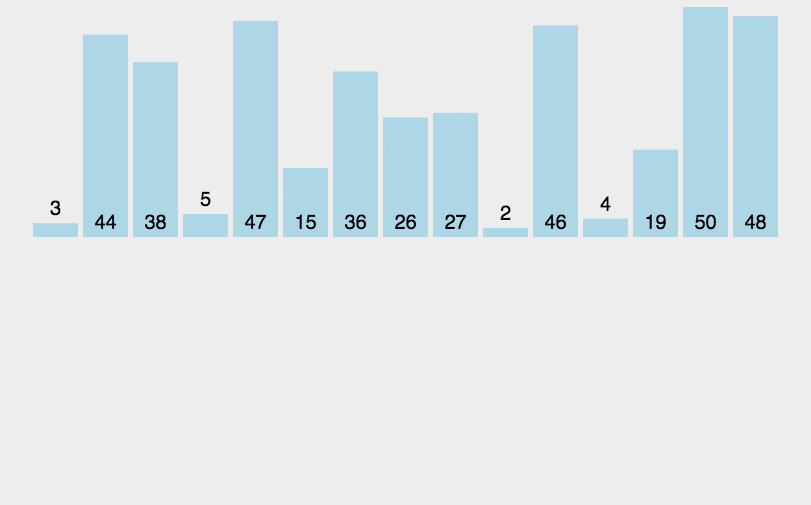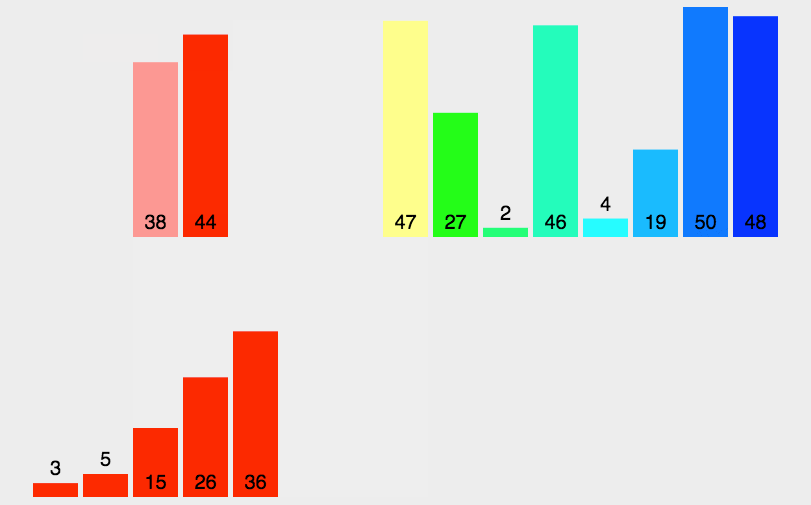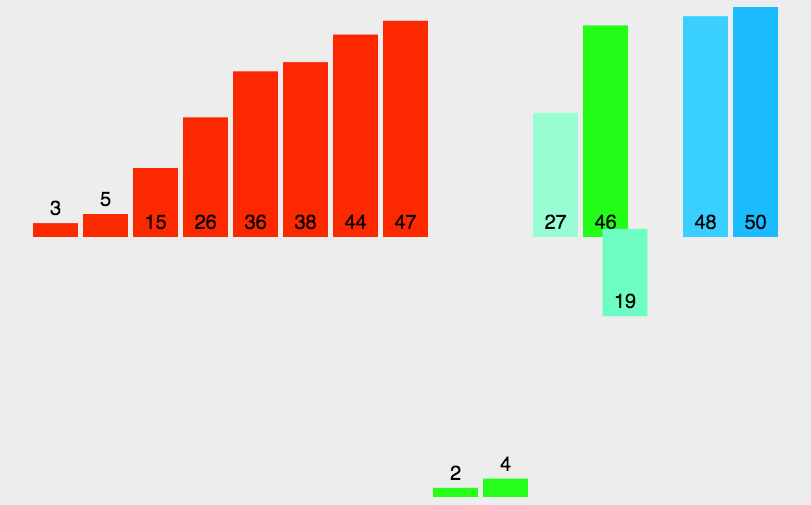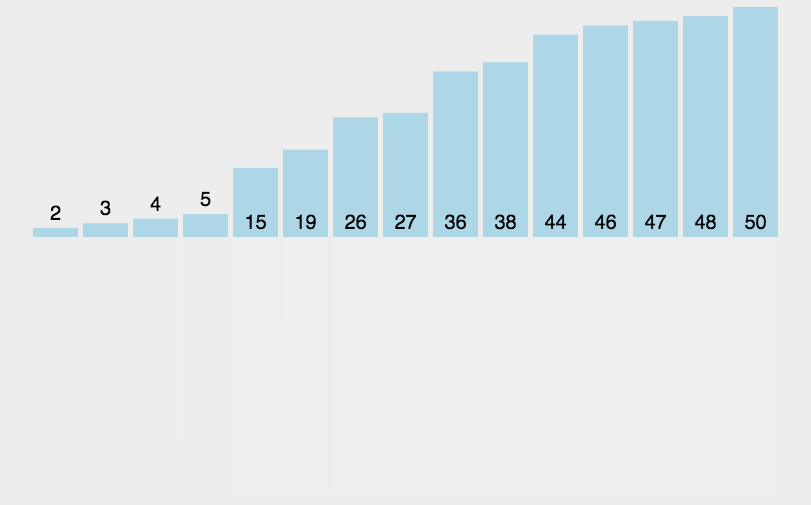
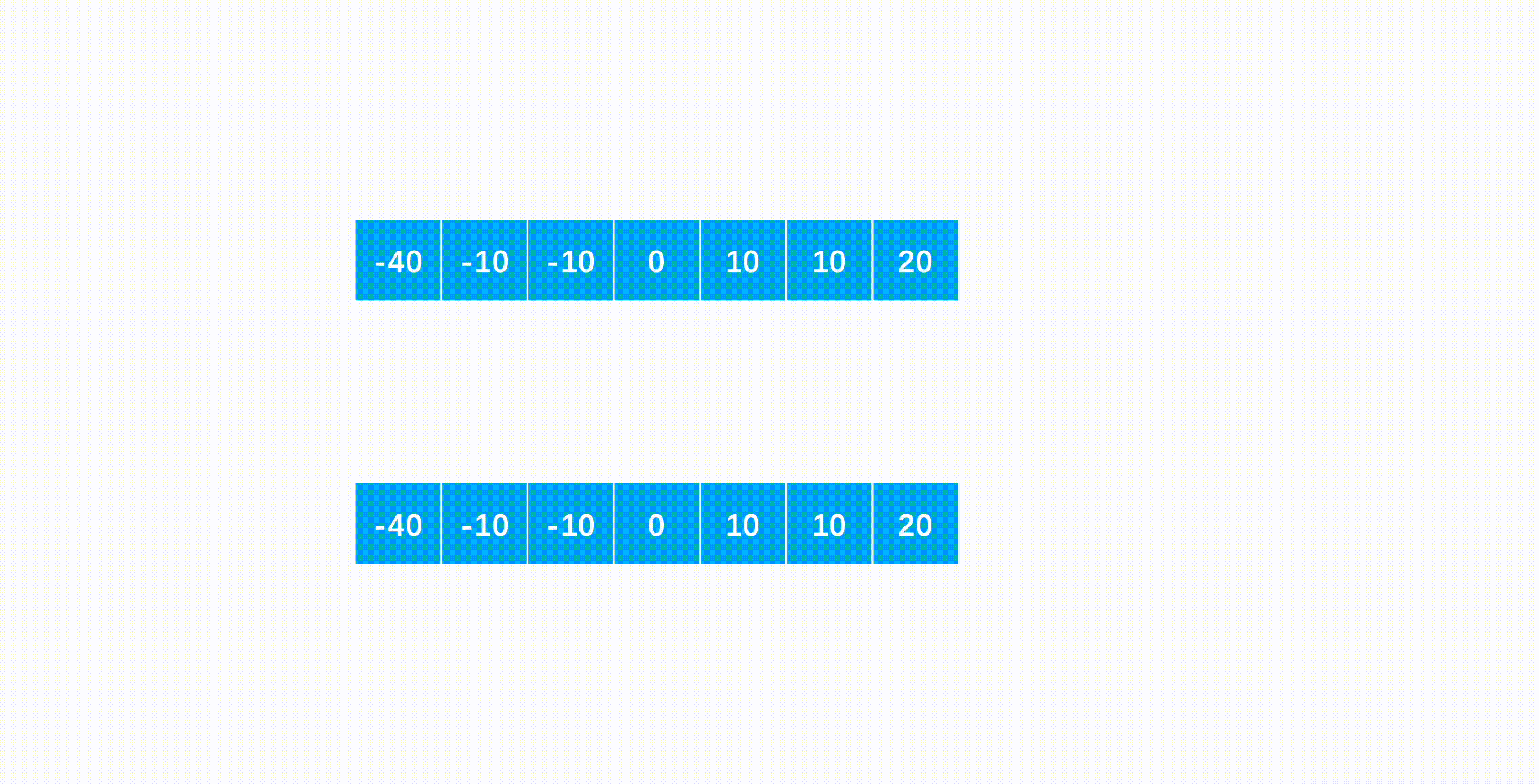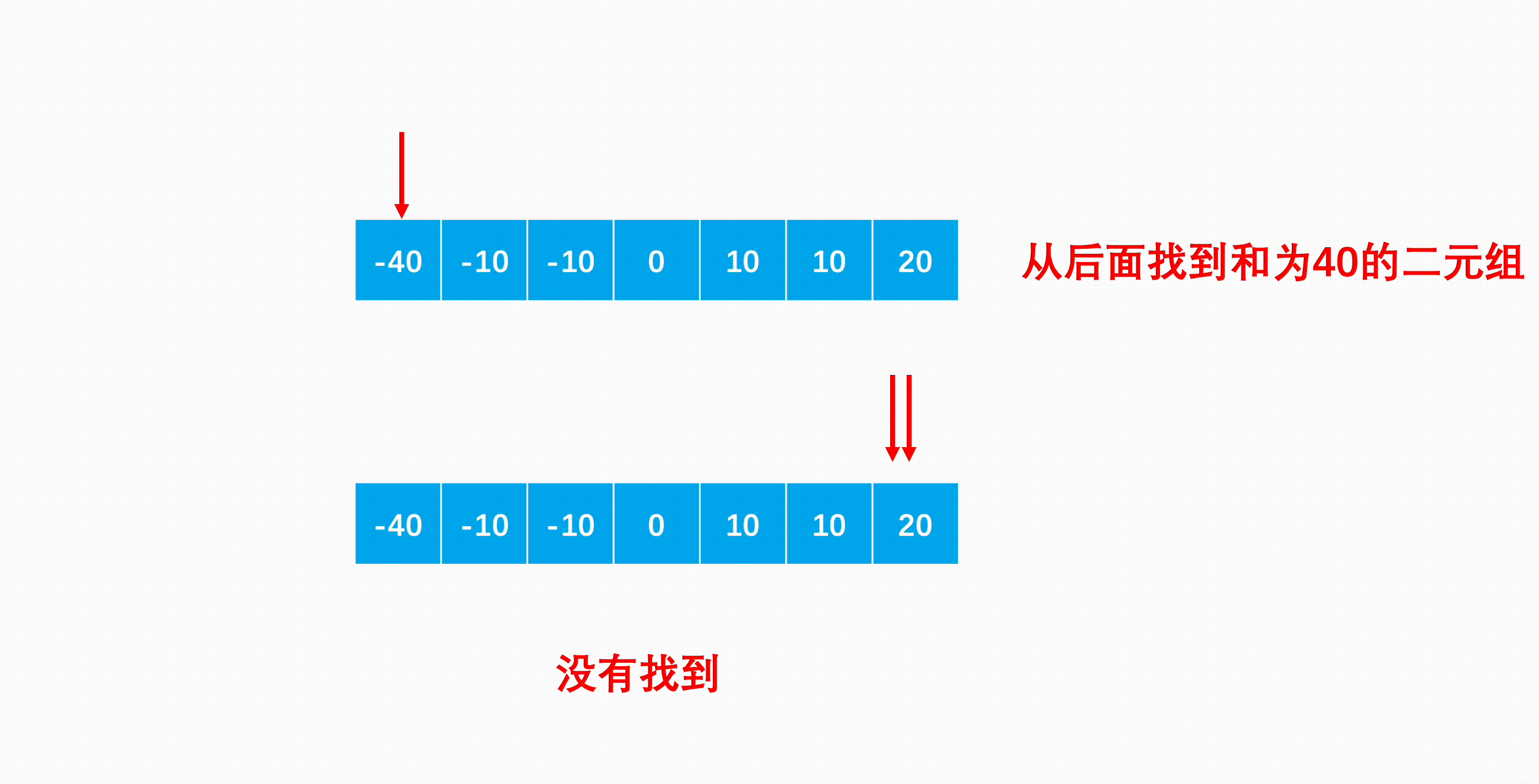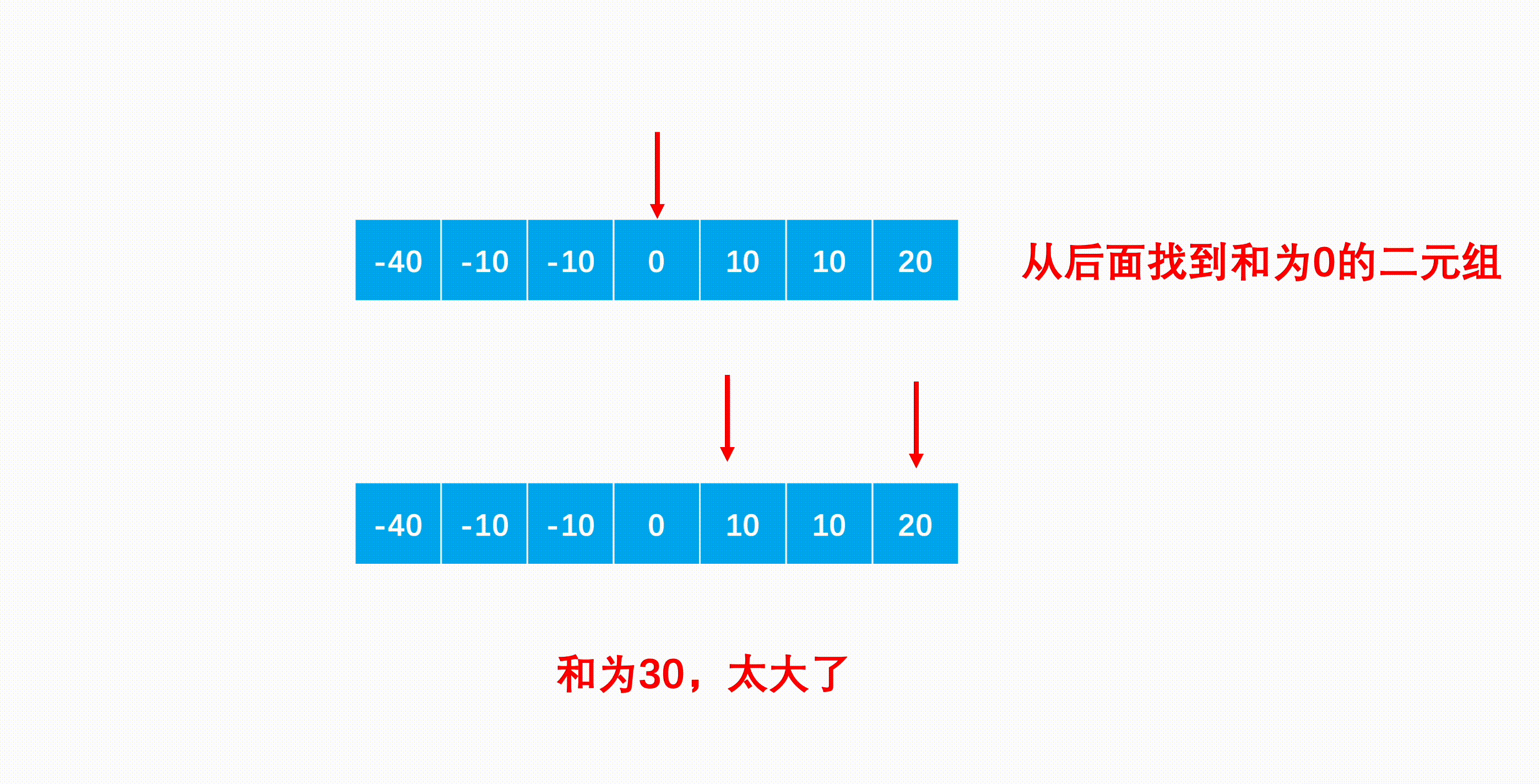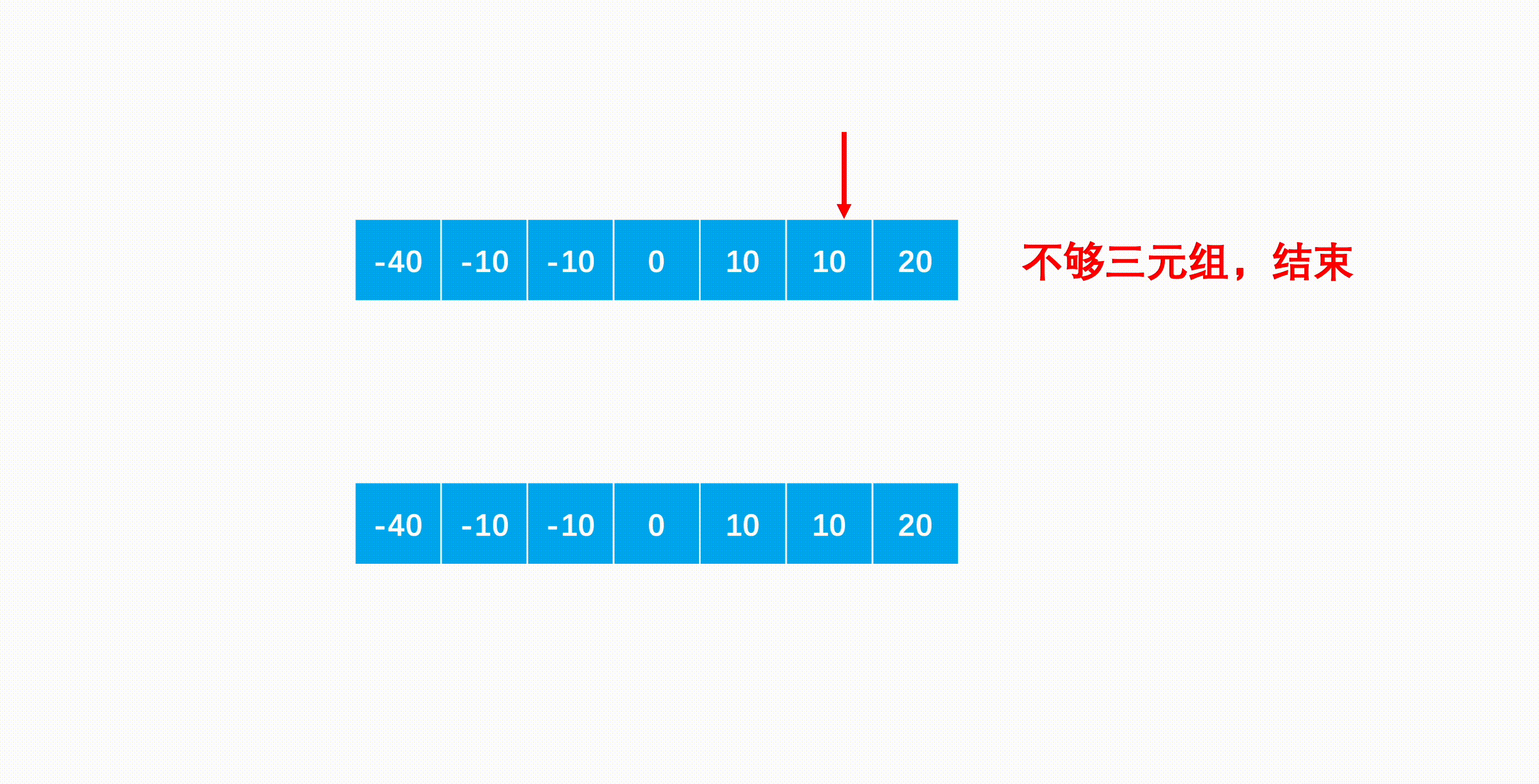刷题笔记

算法 评论

洛谷

P1059 [NOIP2006 普及组] 明明的随机数

数组去重排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;

int main()
{
    int m;cin >> m;
    int a[m];
    for(int i = 0;i < m;i++)  cin >> a[i];
    sort(a, a + m);  // 排序
    int n = unique(a, a + m) - a;  //去重
    cout << n << endl;
    for(int i = 0;i < n;i++)
        cout << a[i] << " ";
}
//unique(a, a+m)的返回值是a[m]的地址

牛客

BM1 反转链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    ListNode* ReverseList(ListNode* pHead) {
    if(!pHead || !pHead->next)
        return pHead;
    else{
        ListNode *p = pHead,*r = pHead->next, *q = p;
        while(r->next){
            p->next = r->next;
            r->next = q;
            q = r;
            r = p->next;
        }
        r->next = q;
        p->next = NULL;
        pHead = r;
    }
        return pHead;
    }
};

二分查找/排序

BM17 二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int high = nums.size(), mid = high / 2, left = 0;
        if(!high)  return -1;
        while(left <= high){
            mid = (left + high)/2;
            if(nums[mid] == target)
                return mid;
            else if(nums[mid] < target)
                left = mid + 1;
            else
                high = mid-1;
        }
        return -1;
    }
};

BM18 二维数组中的查找

​ 在一个二维数组array中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。

[[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]]

给定 target = 7，返回 true；给定 target = 3，返回 false。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    bool Find(vector<vector<int> > array,int target) {
        int m, n, x, y;
        m = array.size();	//行数
        n = array[0].size();	//列数
        x = m-1;y = 0;	//坐标定在左下角
        while(x >= 0 && y <= n-1){
          if(target < array[x][y])
                   x--;	//遇小上移
          else if(target > array[x][y])
                   y++;	//遇大右移
          else
               return true;
      }
       return false; 
    }
};

BM19 寻找峰值

​ 给定一个长度为n的数组nums，请找到峰值并返回其索引。数组可能包含多个峰值，在这种情况下，返回任何一个所在位置即可。

1.峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于

2.假设 nums[-1] = nums[n] = -\infty−∞

3.对于所有有效的 i 都有 nums[i] != nums[i + 1]

4.你可以使用O(logN)的时间复杂度实现此问题吗？

输入[2,4,1,2,7,8,4]时，会形成两个山峰，一个是索引为1，峰值为4的山峰，另一个是索引为5，峰值为8的山峰。

二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int left = 0;
        int right = nums.size() - 1;
        //二分法 fast-template
        while(left < right){
            int mid = (left + right) / 2;
            //右边是往下，不一定有坡峰
            if(nums[mid] > nums[mid + 1])
                right = mid;
            //右边是往上，一定能找到波峰
            else
                left = mid + 1;
        }
        //其中一个波峰
        return right;}
};

BM20 数组中的逆序对

描述：数组中两个数，如果前一个数字大于后面的数字，则这两数组成一个逆序对。

输入一个数组,求出这个数组中的逆序对的总数P。输出P mod 1000000007的结果。

要求：空间复杂度 O(n)，时间复杂度 O(nlogn)

输入描述：题目保证输入的数组中没有的相同的数字

输入示例 返回值
[1,2,3,4,5,6,7,0] 7
[1,2,3] 0

归并排序

img 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
private:
    const int kmod = 1000000007;
public:
    int InversePairs(vector<int> data) {
        int ret = 0;
        // 在最外层开辟数组
        vector<int> tmp(data.size());
        merge_sort__(data, tmp, 0, data.size() - 1, ret);
        return ret;
    }

    void merge_sort__(vector<int> &arr, vector<int> &tmp, int l, int r, int &ret) {
        if (l >= r) 
            return;
        int mid = l + ((r - l) >> 1);
        merge_sort__(arr, tmp, l, mid, ret);
        merge_sort__(arr, tmp, mid + 1, r, ret);
        merge__(arr, tmp, l, mid, r, ret);
    }

    void merge__(vector<int> &arr, vector<int> &tmp, int l, int mid, int r, int &ret) {
        int i = l, j = mid + 1, k = 0;

        while (i <= mid && j <= r) {
            if (arr[i] > arr[j]) {
                tmp[k++] = arr[j++];
                ret += (mid - i + 1);
                ret %= kmod;
            }
            else
                tmp[k++] = arr[i++];
        }
        while (i <= mid)
            tmp[k++] = arr[i++];
        while (j <= r)
            tmp[k++] = arr[j++];
        for (k = 0, i = l; i <= r; ++i, ++k)
            arr[i] = tmp[k];
    }
};

BM21 旋转数组的最小数字

描述

有一个长度为 n 的非降序数组，比如[1,2,3,4,5]，将它进行旋转，即把一个数组最开始的若干个元素搬到数组的末尾，变成一个旋转数组，比如变成了[3,4,5,1,2]，或者[4,5,1,2,3]这样的。请问，给定这样一个旋转数组，求数组中的最小值。

要求：空间复杂度：O(1)，时间复杂度：O(logn)

输入：[3,4,5,1,2] 返回值：1

输入：[3,100,200,3] 返回值：3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//二分法
class Solution {
public:
    int minNumberInRotateArray(vector<int> rotateArray) {
        int left = 0;
        int right = rotateArray.size() - 1;
        while(left < right){
            int mid = (left + right) / 2;
            //最小的数字在mid右边
            if(rotateArray[mid] > rotateArray[right]) 
                left = mid + 1;
            //无法判断，一个一个试
            else if(rotateArray[mid] == rotateArray[right]) 
                right--;
            //最小数字要么是mid要么在mid左边
            else 
                right = mid;
        }
        return rotateArray[left];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
//遍历
class Solution {
public:
    int minNumberInRotateArray(vector<int> rotateArray) {
        int res = INT_MAX;
        //遍历数组
        for(int i = 0; i < rotateArray.size(); i++) 
            //每次维护最小值
            res = min(res, rotateArray[i]); 
        return res;
    }
};

BM22 比较版本号

**描述:**比较版本号version1和version2的大小。

版本号是由修订号组成，修订号与修订号之间由一个”.”连接。1个修订号可能有多位数字组成，修订号可能包含前导0，且是合法的。例如，1.02.11，0.1，0.2都是合法的版本号。每个版本号至少包含1个修订号。修订号从左到右编号，下标从0开始，最左边的修订号下标为0，下一个修订号下标为1，以此类推。

比较规则：

一. 比较版本号时，请按从左到右的顺序依次比较它们的修订号。比较修订号时，只需比较忽略任何前导零后的整数值。比如”0.1”和”0.01”的版本号是相等的

二. 如果版本号没有指定某个下标处的修订号，则该修订号视为0。例如，”1.1”的版本号小于”1.1.1”。因为”1.1”的版本号相当于”1.1.0”，第3位修订号的下标为0，小于1

三. version1 > version2 返回1，如果 version1 < version2 返回-1，不然返回0.

1
2
输入："1.1","1.01"		返回值：0
说明：version2忽略前导0，为"1.1"，和version相同，返回0 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int compare(string version1, string version2) {
        int n1 = version1.size();
        int n2 = version2.size();
        int i = 0, j = 0;
        //直到某个字符串结束
        while(i < n1 || j < n2){
            long long num1 = 0;
            //从下一个点前截取数字
            while(i < n1 && version1[i] != '.'){ 
                num1 = num1 * 10 + (version1[i] - '0');
                i++;
            }
            //跳过点
            i++; 
            long long num2 = 0;
            //从下一个点前截取数字
            while(j < n2 && version2[j] != '.'){ 
                num2 = num2 * 10 + (version2[j] - '0');
                j++;
            }
            //跳过点
            j++; 
            //比较数字大小
            if(num1 > num2) 
                return 1;
            if(num1 < num2)
                return -1;
        }
        //版本号相同
        return 0; 
    }
};

二叉树

BM27 按之字形顺序打印二叉树

翻转数组！！！

1
2
if(flag)
        reverse(row.begin(), row.end());

栈方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
  public:
    vector<vector<int> > Print(TreeNode* pRoot) {
        vector<vector<int> > res;
        if (pRoot == NULL)   //如果是空，则直接返回空vector
            return res;
        stack<TreeNode*> q, q2;     //队列存储，进行层次遍历
        q.push(pRoot);
        TreeNode* cur;
        int tag = 1;
        while (!q.empty() || !q2.empty()) {
            //记录二叉树的某一行
            vector<int> row;
            int n = tag ? q.size() : q2.size();
            //因先进入的是根节点，故每层节点多少，队列大小就是多少
            for (int i = 0; i < n; i++) {
                cur = (tag) ? q.top() : q2.top();
                if (tag)  q.pop();
                else  q2.pop();
                row.push_back(cur->val);
                //若是左右孩子存在，则存入左右孩子作为下一个层次
                if (tag) {
                    if (cur->left)
                        q2.push(cur->left);
                    if (cur->right)
                        q2.push(cur->right);
                } else {
                    if (cur->right)
                        q.push(cur->right);
                    if (cur->left)
                        q.push(cur->left);
                }
            }
            tag = !tag;
            //每一层加入输出
            res.push_back(row);
        }
        return res;
    }
};

BM28 二叉树的最大深度

求给定二叉树的最大深度，深度是指树的根节点到任一叶子节点路径上节点的数量。

最大深度是所有叶子节点的深度的最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
  public:
    /**
     *
     * @param root TreeNode类
     * @return int整型
     */
    int maxDepth(TreeNode* root) {
        // write code here
        if (!root) {
            return 0;
        }
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

BM29 二叉树中和为某一值的路径(一)

给定一个二叉树root和一个值 sum ，判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。

1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点

2.叶子节点是指没有子节点的节点

3.路径只能从父节点到子节点，不能从子节点到父节点

4.总节点数目为n

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool hasPathSum(TreeNode* root, int sum) {
        //空节点找不到路径
        if(root == NULL) 
            return false;
        //叶子节点，且路径和为sum
        if(root->left == NULL && root->right == NULL && sum - root->val == 0) 
            return true;
        //递归进入子节点
        return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
    }
};

堆/栈/队列

BM42 用两个栈实现队列

保证操作合法，即保证pop操作时队列内已有元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution
{
public:
    void push(int node) {
        stack1.push(node);
    }

    int pop() {
        if(stack2.empty()){
            while(!stack1.empty()){
                stack2.push(stack1.top());
                stack1.pop();
        }
        }
        int node = stack2.top();
        stack2.pop();
        return node;
    }

private:
    stack<int> stack1;
    stack<int> stack2;
};

BM43 包含min函数的栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    stack<int> s1;
    stack<int> s2;

    void push(int value) {
        s1.push(value);
        if(s2.empty() || s2.top() > value){
            s2.push(value);
        }
        else{
            s2.push(s2.top());
        }
    }
    void pop() {
        s1.pop();
        s2.pop();
    }
    int top() {
        return s1.top();
    }
    int min() {
        return s2.top();
    }
};

BM44 有效括号序列

给出一个仅包含字符’(‘,’)’,’{‘,’}’,’[‘和’]’,的字符串，判断给出的字符串是否是合法的括号序列
括号必须以正确的顺序关闭，”()”和”()[]{}”都是合法的括号序列，但”(]”和”([)]”不合法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    bool isValid(string s) {
        //辅助栈
        stack<char> st; 
        //遍历字符串
        for(int i = 0; i < s.length(); i++){ 
            //遇到左小括号
            if(s[i] == '(') 
                //期待遇到右小括号
                st.push(')'); 
            //遇到左中括号
            else if(s[i] == '[') 
                //期待遇到右中括号
                st.push(']'); 
            //遇到左打括号
            else if(s[i] == '{')
                //期待遇到右打括号 
                st.push('}'); 
            //必须有左括号的情况下才能遇到右括号
            else if(st.empty()) 
                return false;
            //右括号匹配则弹出
            else if(st.top() == s[i]) 
                st.pop();
        }
        //栈中是否还有元素
        return st.empty(); 
    }
};

BM45 滑动窗口的最大值

  1. 遍历数组的每一个元素，
  2. 如果容器为空，则直接将当前元素加入到容器中。
  3. 如果容器不为空，则让当前元素和容器的最后一个元素比较，如果大于，则将容器的最后一个元素删除，然后继续将当前元素和容器的最后一个元素比较
  4. 如果当前元素小于容器的最后一个元素，则直接将当前元素加入到容器的末尾
  5. 如果容器头部的元素已经不属于当前窗口的边界，则应该将头部元素删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<int> maxInWindows(const vector<int>& num, unsigned int size)
    {
        vector<int> ret;
        if (num.size() == 0 || size < 1 || num.size() < size) return ret;
        int n = num.size();
           deque<int> dq;
           for (int i = 0; i < n; ++i) {
               while (!dq.empty() && num[dq.back()] < num[i]) {
                   dq.pop_back();
               }
               dq.push_back(i);
               // 判断队列的头部的下标是否过期
               if (dq.front() + size <= i) {
                   dq.pop_front();
            }
            // 判断是否形成了窗口
               if (i + 1 >= size) {
                   ret.push_back(num[dq.front()]);
               }
           }
           return ret; 
    }
};

BM46 最小的K个数

给定一个长度为 n 的可能有重复值的数组，找出其中不去重的最小的 k 个数。例如数组元素是4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4(任意顺序皆可)。

方法一：直接排序

直接排序，取前k个元素。

1
2
3
4
5
6
7
8
9
class Solution {
public:
    vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
        vector<int> ret;
        if (k==0 || k>input.size()) return ret;
        sort(input.begin(), input.end());
        return vector<int>({input.begin(), input.begin()+k});   
    }
};

方法二：堆排序

建立一个容量为k的大根堆的优先队列。遍历一遍元素，如果队列大小<k，就直接入队，否则，让当前元素与队顶元素相比，如果队顶元素大，则出队，将当前元素入队

优先队列 优先队列 - 知乎

优先队列中，队列中的数据被赋予了优先级。当访问元素时，优先级最高的会先被删除。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
        vector<int> ret;
        if (k==0 || k > input.size()) return ret;
        priority_queue<int, vector<int>> pq;
        for (const int val : input) {
            if (pq.size() < k) {
                pq.push(val);
            }
            else {
                if (val < pq.top()) {
                    pq.pop();
                    pq.push(val);
                }
            }
        }
        while (!pq.empty()) {
            ret.push_back(pq.top());
            pq.pop();
        }
        return ret;
    }
};

方法三：快排思想

快速排序 视频讲解

分治法思想

对数组[l, r]一次快排partition过程可得到，[l, p), p, [p+1, r)三个区间,[l,p)为小于等于p的值
[p+1,r)为大于等于p的值。然后再判断p，利用二分法

  1. 如果[l,p), p，也就是p+1个元素（因为下标从0开始），如果p+1 == k, 找到答案
  2. 如果p+1 < k, 说明答案在[p+1, r)区间内，
  3. 如果p+1 > k , 说明答案在[l, p)内
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int partition(vector<int> &input, int l, int r) {
        int pivot = input[r-1];
        int i = l;
        for (int j=l; j<r-1; ++j) {
            if (input[j] < pivot) {
                swap(input[i++], input[j]);
            }
        }
        swap(input[i], input[r-1]);
        return i;

    }
    vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
        vector<int> ret;
        if (k==0 || k > input.size()) return ret;
         int l = 0, r = input.size();
        while (l < r) {
            int p = partition(input, l, r);
            if (p+1 == k) {
                return vector<int>({input.begin(), input.begin()+k});
            }
            if (p+1 < k) {
                l = p + 1;
            }   
            else {
                r = p;
            }

        }c
        return ret;
    }
};

寻找第K大

有一个整数数组，请你根据快速排序的思路，找出数组中第 k 大的数。

给定一个整数数组 a ,同时给定它的大小n和要找的 k ，请返回第 k 大的数(包括重复的元素，不用去重)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    int partion(vector<int>& a, int low, int high){ //常规的快排划分，但这次是大数在左
        int temp = a[low];
        while(low < high){
            while(low < high && a[high] <= temp)
                high--;
            if(low == high)
                break;
            else
                a[low] = a[high];
            while(low < high && a[low] >= temp)
                low++;
            if(low == high)
                break;
            else
                a[high] = a[low];
        }
        a[low] = temp;
        return low;
    }
    
    int quickSort(vector<int>& a, int low, int high, int K){
        int p = partion(a, low, high); //先进行一轮划分，p下标左边的都比它大，下标右边都比它小
        if(K == p - low + 1)  //若p刚好是第K个点，则找到
            return a[p];
        else if(p - low + 1 > K)  //从头到p超过k个数组，则目标在左边
            return quickSort(a, low, p - 1, K);  //递归左边
        else  
            return quickSort(a, p + 1, high, K - (p - low + 1));  //否则，在右边,递归右边,但是需要减去左边更大的数字的数量
    }
    
    int findKth(vector<int> a, int n, int K) {
        return quickSort(a, 0, n - 1, K);
    }
};

BM48 数据流中的中位数

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，使用GetMedian()方法获取当前读取数据的中位数。

插入排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    //记录输入流
    vector<int> val;
    void Insert(int num) {
        if(val.empty())
            //val中没有数据，直接加入
            val.push_back(num); 
        //val中有数据，需要插入排序
        else{
            int i = 0;
            //遍历找到插入点
            for(; i < val.size(); i++){
                if(num <= val[i]){
                   break;
                }
            }
            val.insert(val.begin() + i, num);
        }
    }
    double GetMedian() {
        int n = val.size();
        //奇数个数字
        if(n % 2 == 1){ 
            //类型转换
            return double(val[n / 2]); 
        }
        //偶数个数字
        else{ 
            double a = val[n / 2];
            double b = val[n / 2 - 1];
            return (a + b) / 2;
        }
    }
};

堆排序（优先队列）

  • 一个大根堆，存中位数左边的数据，
  • 一个小根堆，存中位数右边的数据，
  • 动态维护两个数据结构的大小，即最多只相差一个。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//版本一
class Solution {
public:
    //大顶堆，元素数值较小
    priority_queue<int> min; 
    //小顶堆，元素数值都比大顶堆大
    priority_queue<int, vector<int>, greater<int>> max;
    //维护两个堆，取两个堆顶部即可
    void Insert(int num) {       
        //先加入较小部分 
        min.push(num);
        //将较小部分的最大值取出，送入到较大部分
        max.push(min.top());  
        min.pop();
        //平衡两个堆的数量
        if(min.size() < max.size()){  
            min.push(max.top());
            max.pop();
        }        
    }
    double GetMedian() {
        //奇数个
        if(min.size() > max.size())  
            return (double)min.top();
        else
            //偶数个
            return (double)(min.top() + max.top()) / 2; 
    }
};

BM49 表达式求值

请写一个整数计算器，支持加减乘三种运算和括号。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution {
public:
    vector<int> function(string s, int index){
        stack<int> stack; 
        int num = 0;
        char op = '+';
        int i;
        for(i = index; i < s.length(); i++){
            //数字转换成int数字
            if(isdigit(s[i])){
                num = num * 10 + s[i] - '0';
                if(i != s.length() - 1)
                    continue;
            }
            //碰到'('时，把整个括号内的当成一个数字处理
            if(s[i] == '('){
                //递归处理括号
                vector<int> res = function(s, i + 1);
                num = res[0];
                i = res[1];
                if(i != s.length() - 1)
                    continue;
            }           
            switch(op){
            //加减号先入栈
            case '+': 
                stack.push(num);
                break;
            case '-':
                //相反数
                stack.push(-num);
                break;
            //优先计算乘号
            case '*':  
                int temp = stack.top();
                stack.pop();
                stack.push(temp * num);
                break;
            }
            num = 0;
            //右括号结束递归
            if(s[i] == ')')
                break; 
            else 
                op = s[i];
        }
        int sum = 0;
        //栈中元素相加
        while(!stack.empty()){  
            sum += stack.top();
            stack.pop();
        }
        return vector<int> {sum, i}; 
    }
    
    int solve(string s) {
        return function(s, 0)[0];
    }
};

哈希

BM 50 两数之和

哈希表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        int n = numbers.size(); 
        vector <int> res;
        if (!n) 	return res;
        // unordered_map是用哈希表实现的，复杂度为O(1)，而map是用红黑树实现的
        unordered_map<int, int> hashmap; 
        for (int i = 0; i < n; i ++) {
            if (hashmap.find(target - numbers[i]) != hashmap.end()) { 
                // find函数返回hashmap.end()代表未找到，否则代表找到
                // 将结果存入数组
                res.push_back(hashmap[target - numbers[i]] + 1); 
                res.push_back(i + 1);
                break;
            } else {
                hashmap[numbers[i]] = i; // 将未找到的值插入哈希表中，继续遍历
            }
        }
        return res;
    }
};

BM51 数组中出现次数超过一半的数字

哈希表

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        unordered_map<int,int> mp;
        for (const int val : numbers) ++mp[val];
        for (const int val : numbers) {
            if (mp[val] > numbers.size() / 2 ) return val;
        }
        return 0;
    }
};
//时间复杂度：O(n)
//空间复杂度：O(n)

排序法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        sort(numbers.begin(), numbers.end());
        int cond = numbers[numbers.size() / 2];
        int cnt = 0;
        for (const int k :numbers) {
            if (cond == k) ++cnt;
        }
        if (cnt > numbers.size() / 2) return cond;
        return 0;
    }
};
//时间复杂度：O(nlongn)
//空间复杂度：O(1)

候选法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        int cond = -1;
        int cnt = 0;
        for (int i=0; i<numbers.size(); ++i) {
            if (cnt == 0) {
                cond = numbers[i];
                ++cnt;
            }
            else {
                if (cond == numbers[i]) ++cnt;
                else --cnt;
            }

        }
        cnt = 0;
        for (const int k :numbers) {
            if (cond == k) ++cnt;
        }
        if (cnt > numbers.size() / 2) return cond;
        return 0;
    }
};
//时间复杂度：O(n)
//空间复杂度：O(1)

BM52 数组中只出现一次的两个数字

哈希表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<int> FindNumsAppearOnce(vector<int>& array) {
        unordered_map<int, int> mp;
        vector<int> res;
        //遍历数组
        for(int i = 0; i < array.size(); i++) 
            //统计每个数出现的频率
            mp[array[i]]++; 
        //再次遍历数组
        for(int i = 0; i < array.size(); i++) 
            //找到频率为1的两个数
            if(mp[array[i]] == 1) 
                res.push_back(array[i]);
        //整理次序
        if(res[0] < res[1]) 
            return res;
        else
            return {res[1], res[0]};
    }
};
//时间复杂度：O(n)，其中n为数组长度，两次单独的遍历数组每个元素
//空间复杂度：O(n)，哈希表的长度应该为(n−2)/2

异或运算

​ 异或运算满足交换率，且相同的数字作异或会被抵消掉，比如：a⊕b⊕c⊕b⊕c=a，且任何数字与0异或还是原数字，该题目里面所有数字异或运算就会得到a⊕b，也即得到了两个只出现一次的数字的异或和。

1
2
3
4
//遍历数组得到a^b
for(int i = 0; i < array.length; i++) 
    temp ^= array[i];
//
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<int> FindNumsAppearOnce(vector<int>& array) {
        vector<int> res(2, 0);
        int temp = 0;
        //遍历数组得到a^b
        for(int i = 0; i < array.size(); i++) 
            temp ^= array[i];
        int k = 1;
        //找到两个数不相同的第一位
        while((k & temp) == 0) 
            k <<= 1;
        for(int i = 0; i < array.size(); i++){
            //遍历数组，对每个数分类
            if((k & array[i]) == 0) 
                res[0] ^= array[i];
            else
                res[1] ^= array[i];
        }
        //整理次序
        if(res[0] < res[1]) 
            return res;
        else
            return {res[1], res[0]};
    }
};
//时间复杂度：O(n)，遍历两次数组，找到两个数不相同的第一位循环为常数次
//空间复杂度：O(1)，常数级变量使用，无额外辅助空间

BM53 缺失的第一个正整数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int minNumberDisappeared(vector<int>& nums) {
        int n = nums.size();
        unordered_map<int, int> mp;
        //哈希表记录数组中出现的每个数字
        for(int i = 0; i < n; i++) 
            mp[nums[i]]++;
        int res = 1;
        //从1开始找到哈希表中第一个没有出现的正整数
        while(mp.find(res) != mp.end()) 
            res++;
        return res;
    }
};
//时间复杂度：O(n)
//空间复杂度：O(n)

原地哈希

  • step 1：我们可以先遍历数组将所有的负数都修改成n+1。
  • step 2：然后再遍历数组，每当遇到一个元素绝对值不超过n时，则表示这个元素是1～n中出现的元素，我们可以将这个数值对应的下标里的元素改成负数，相当于每个出现过的正整数，我们把与它值相等的下标都指向一个负数，这就是类似哈希表的实现原理的操作。
  • step 3：最后遍历数组的时候碰到的第一个非负数，它的下标就是没有出现的第一个正整数，因为它在之前的过程中没有被修改，说明它这个下标对应的正整数没有出现过。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int minNumberDisappeared(vector<int>& nums) {
        int n = nums.size();
        //遍历数组
        for(int i = 0; i < n; i++) 
            //负数全部记为n+1
            if(nums[i] <= 0) 
                nums[i] = n + 1;
        for(int i = 0; i < n; i++)
            //对于1-n中的数字
            if(abs(nums[i]) <= n) 
                //这个数字的下标标记为负数
                nums[abs(nums[i]) - 1] = -1 * abs(nums[abs(nums[i]) - 1]); 
        for(int i = 0; i < n; i++)
            //找到第一个元素不为负数的下标
            if(nums[i] > 0)
                return i + 1;
        return n + 1;
    }
};
//时间复杂度：O(n)
//空间复杂度：O(1)

三数之和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<vector<int> > threeSum(vector<int> &num) {
        vector<vector<int>>ans;
        if(num.size()<3)return ans;
        sort(num.begin(),num.end());
        
        for(int i = 0; i < num.size() - 2; i++){
            if(num[i] == num[i-1] && i)	continue;
            int l = i + 1,r = num.size() - 1;
            while(l < r){
                if(num[l] + num[r] == -num[i]){
                    //若指针i 加指针j 等于当前数x 则答案为x 和指针i 与j 的三元组
                    ans.push_back({num[i],num[l],num[r]});
                    while(num[l]==num[l+1] && l + 1<r)	l++;
                    while(num[r]==num[r-1] && r-1 > l)	r--;
                    l++;
                    r--;
                }
                else if(num[l]+num[r]>-num[i]){
                    r--;	//若指针l 加指针r 大于当前数-num[i]则指针r--
                }
                else l++;	//若指针l 加指针r 小于当前数-num[i]则指针l++，
            }
        }
        return ans;
    }
};

alt

递归/回溯

BM55 没有重复项数字的全排列

给出一组数字，返回该组数字的所有排列：

例如：

[1,2,3]的所有排列如下
[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2], [3,2,1].
（以数字在数组中的位置靠前为优先级，按字典序排列输出。）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    void recursion(vector<vector<int> > &res, vector<int> &num, int index){
        //分枝进入结尾，找到一种排列
        if(index == num.size() - 1) 
            res.push_back(num);
        else{
            //遍历后续的元素
            for(int i = index; i < num.size(); i++){ 
                //交换二者
                swap(num[i], num[index]); 
                //继续往后找
                recursion(res, num, index + 1); 
                //回溯
                swap(num[i], num[index]); 
            }
        }
    }
    
    vector<vector<int> > permute(vector<int> &num) {
        //先按字典序排序
        sort(num.begin(), num.end()); 
        vector<vector<int> > res;
        //递归获取
        recursion(res, num, 0); 
        return res;
    }
};

alt

BM56 有重复项数字的全排列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    void recursion(vector<vector<int> > &res, vector<int> &num, vector<int> &temp, vector<int> &vis){
        //临时数组满了加入输出
        if(temp.size() == num.size()){ 
            res.push_back(temp);
            return;
        }
        //遍历所有元素选取一个加入
        for(int i = 0; i < num.size(); i++){ 
            //如果该元素已经被加入了则不需要再加入了
            if(vis[i]) 	continue;
            if(i > 0 && num[i - 1] == num[i] && !vis[i - 1]) 
                //当前的元素num[i]与同一层的前一个元素num[i-1]相同且num[i-1]已经用过了
                continue;  
            //标记为使用过
            vis[i] = 1;  
            //加入数组
            temp.push_back(num[i]); 
            recursion(res, num, temp, vis);
            //回溯
            vis[i] = 0; 
            temp.pop_back();
        }
    }
    
    vector<vector<int> > permuteUnique(vector<int> &num) {
        //先按字典序排序
        sort(num.begin(), num.end()); 
        //标记每个位置的元素是否被使用过
        vector<int> vis(num.size(), 0); 
        vector<vector<int> > res;
        vector<int> temp; 
        //递归获取
        recursion(res, num, temp, vis); 
        return res;
    }
};

alt

BM57 岛屿数量

给一个01矩阵，1代表是陆地，0代表海洋， 如果两个1相邻，那么这两个1属于同一个岛。我们只考虑上下左右为相邻。岛屿: 相邻陆地可以组成一个岛屿（相邻:上下左右） 判断岛屿个数。

例如：输入 (注：存储的01数据其实是字符’0’,’1’)

[[1,1,0,0,0],

[0,1,0,1,1],

[0,0,0,1,1],

[0,0,0,0,0],

[0,0,1,1,1]]

对应的输出为3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
public:
    //深度优先遍历与i，j相邻的所有1
    void dfs(vector<vector<char>>& grid, int i, int j) { 
        int n = grid.size();	//行
        int m = grid[0].size();		//列
        grid[i][j] = '0'; 	 //置为0
        
        //后续四个方向遍历
        if(i - 1 >= 0 && grid[i - 1][j] == '1') 
            dfs(grid, i - 1, j);
        if(i + 1 < n && grid[i + 1][j] == '1') 
            dfs(grid, i + 1,j);
        if(j - 1 >= 0 && grid[i][j - 1] == '1') 
            dfs(grid, i, j - 1);
        if(j + 1 < m && grid[i][j + 1] == '1') 
            dfs(grid, i, j + 1);
    }
    
    int solve(vector<vector<char> >& grid) {
        int n = grid.size();
        //空矩阵的情况
        if (n == 0)  
            return 0;
        int m = grid[0].size();
        //记录岛屿数
        int count = 0; 
        //遍历矩阵
        for(int i = 0; i < n; i++){ 
            for(int j = 0; j < m; j++){
                //遍历到1的情况
                if(grid[i][j] == '1'){ 
                    //计数
                    count++;
                    dfs(grid, i, j); 	//将与这个1相邻的所有1置为0
                }
            }
        }
        return count;
    }
};

alt

BM58 字符串的排列

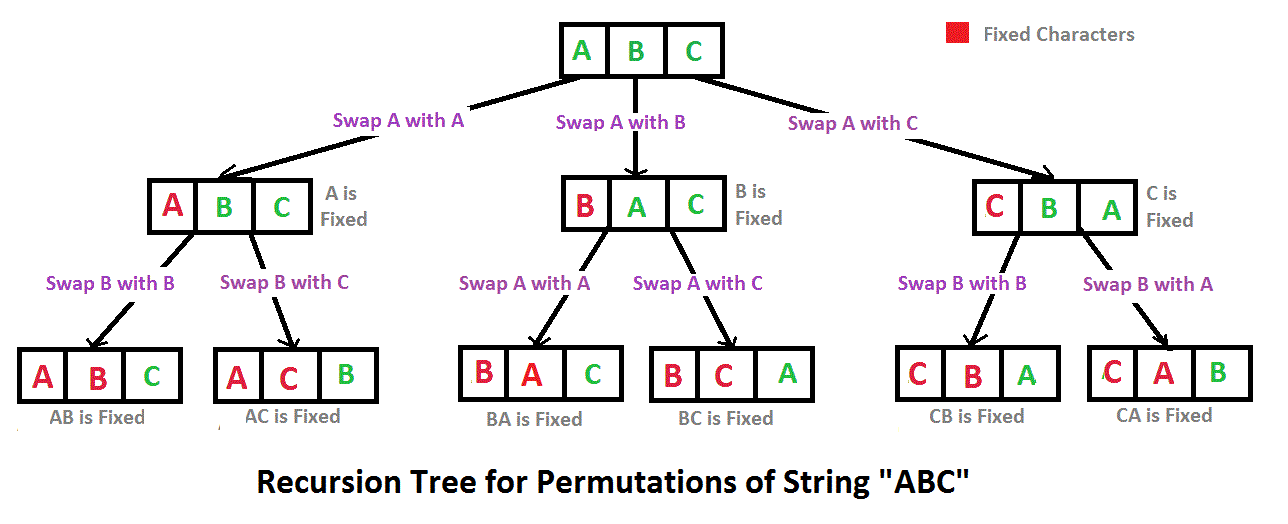
输入一个长度为 n 字符串，打印出该字符串中字符的所有排列，你可以以任意顺序返回这个字符串数组。

例如输入字符串ABC,则输出由字符A,B,C所能排列出来的所有字符串ABC,ACB,BAC,BCA,CBA和CAB。

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    void recursion(vector<string> &res, string &str, string &temp, vector<int> &vis){
        //临时字符串满了加入输出
        if(temp.length() == str.length()){ 
            res.push_back(temp);
            return;
        }
        //遍历所有元素选取一个加入
        for(int i = 0; i < str.length(); i++){ 
            //如果该元素已经被加入了则不需要再加入了
            if(vis[i]) 
                continue;
            if(i > 0 && str[i - 1] == str[i] && !vis[i - 1])
                //当前的元素str[i]与同一层的前一个元素str[i-1]相同且str[i-1]已经用过了
                continue;
            //标记为使用过  
            vis[i] = 1;  
            //加入临时字符串
            temp.push_back(str[i]); 
            recursion(res, str, temp, vis);
            //回溯
            vis[i] = 0; 
            temp.pop_back();
        }
    }
    
    vector<string> Permutation(string str) {
        //先按字典序排序，使重复字符串相邻
        sort(str.begin(), str.end()); 
        //标记每个位置的字符是否被使用过s
        vector<int> vis(str.size(), 0); 
        vector<string> res;
        string temp;
        //递归获取
        recursion(res, str, temp, vis); 
        return res;
    }
};

BM59 N皇后问题

N皇后问题是指在 n * n 的棋盘上要摆 n 个皇后，要求：任何两个皇后不同行，不同列也不在同一条斜线上，求给一个整数 n ，返回 n 皇后的摆法数。

常规代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    //判断皇后是否符合条件
    bool isValid(vector<int> &pos, int row, int col){ 
        //遍历所有已经记录的行
        for(int i = 0; i < row; i++){ 
            //不能同行同列同一斜线
            if(row == i || col == pos[i] || abs(row - i) == abs(col - pos[i])) 
                return false;
        }
        return true;
    }
    
    //递归查找皇后种类
    void recursion(int n, int row, vector<int> & pos, int &res){ 
        //完成全部行都选择了位置
        if(row == n){ 
            res++; 
            return;
        }
        //遍历所有列
        for(int i = 0; i < n; i++){ 
            //检查该位置是否符合条件
            if(isValid(pos, row, i)){ 
                //加入位置
                pos[row] = i; 
                //递归继续查找
                recursion(n, row + 1, pos, res); 
            }
        }
    }
    
    int Nqueen(int n) {
        int res = 0;
        vector<int> pos(n, 0); 	//下标为行号，元素为列号，记录皇后位置 
        recursion(n, 0, pos, res); 	 //递归
        return res;
    }
};

位运算

  1. 如对 col = 0100 对应第二列已有皇后，那么下一行的第一列和第三列都不能选
    对应 pos = 0010，也就是col右移一位；对应neg = 1000，也就是col左移一位
    pre = ~ (col | pos | neg) & ((1 << n) - 1) 代表可以放皇后的位置
    ~ (col | pos | neg)：col、pos、neg取或运算后0表示可以放皇后的位置，取反后1表示可以放皇后的位置((1 << n) - 1) ：是为了保证pre不大于n位
  2. 然后对pre中所有的1进行遍历，从最后一个1开始往前遍历，在当前行放置了一个皇后之后进入下一行，对col、pos、neg做出相应的处理，其余操作与上一个方法相同
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import java.util.*;
public class Solution {
    int res;
    public int Nqueen (int n) {
        limit = (1 << n) - 1;
        backtrack(0, 0, 0, 0, limit);
        return res;
    }
    
    public void backtrack(int i, int col, int pos, int neg, int limit){
        if(i == n){
            res++;
            return;
        }
         //标记放皇后的位置
        int pre = ~(col | pos | neg) & (limit);
        //遍历pre
        while(pre > 0){
            int cur = pre & (-pre);
            //当前行放置了一个皇后之后进入下一行
            backtrack(i + 1, col | cur, (pos | cur) >> 1, (neg | cur) << 1, limit);
            pre &= pre - 1;
        }
    }
}

alt

BM60 括号生成

给出n对括号，请编写一个函数来生成所有的由n对括号组成的合法组合。

例如，给出n=3，解集为：”((()))”, “(()())”, “(())()”, “()()()”, “()(())”

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    void recursion(int left, int right, string temp, vector<string> &res, int n){
        //左右括号都用完了，就加入结果
        if(left == n && right == n){ 
            res.push_back(temp);
            return;
        }
        //使用一次左括号
        if(left < n) 
            recursion(left + 1, right, temp + "(", res, n);
        //使用右括号个数必须少于左括号
        if(right < n && left > right) 
            recursion(left, right + 1, temp + ")", res, n);
    }
    
    vector<string> generateParenthesis(int n) {
        //记录结果
        vector<string> res; 
        //记录每次组装的字符串
        string temp; 
        //递归
        recursion(0, 0, temp, res, n); 
        return res;
    }
};

alt

BM61 矩阵最长递增路径

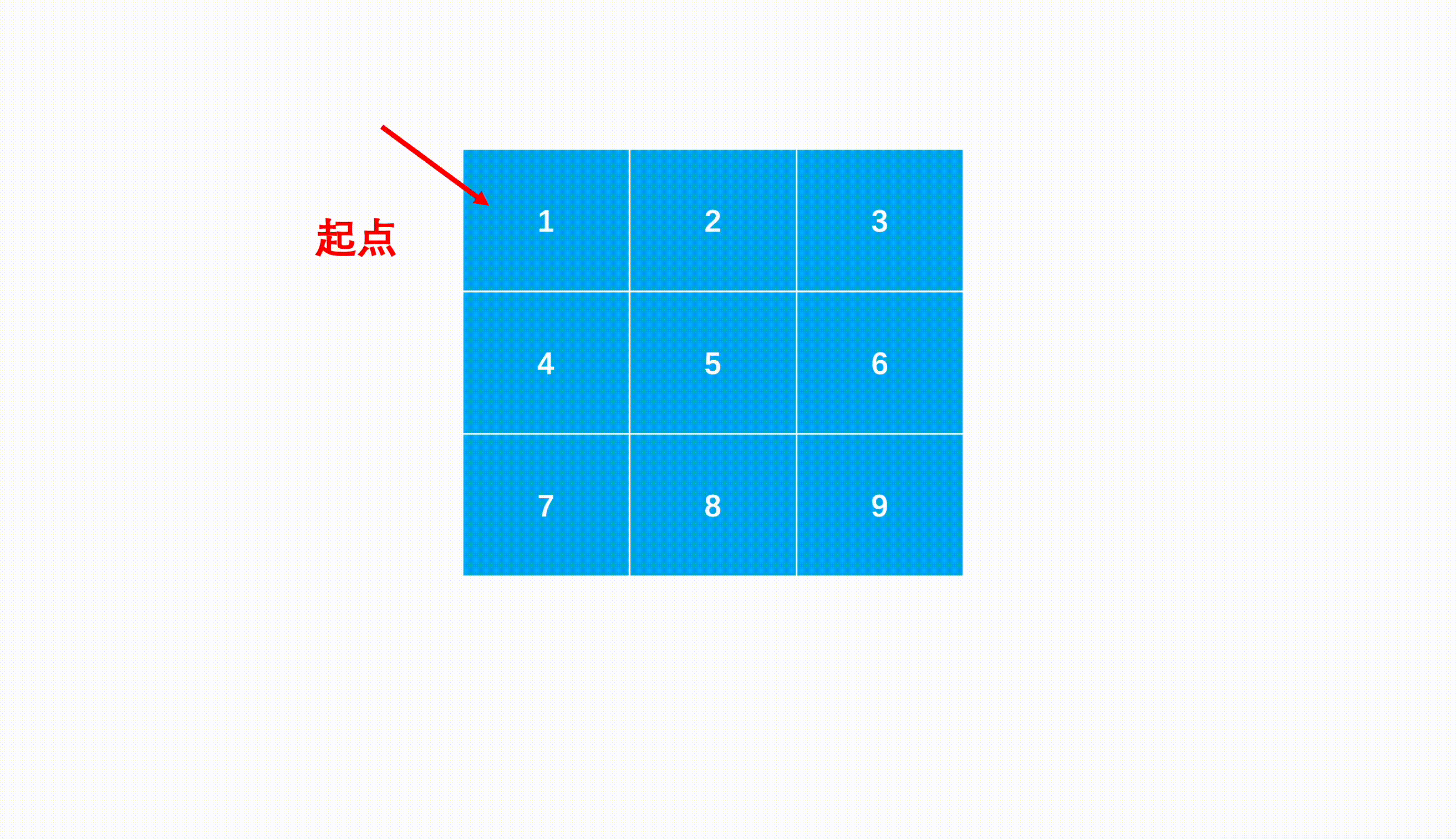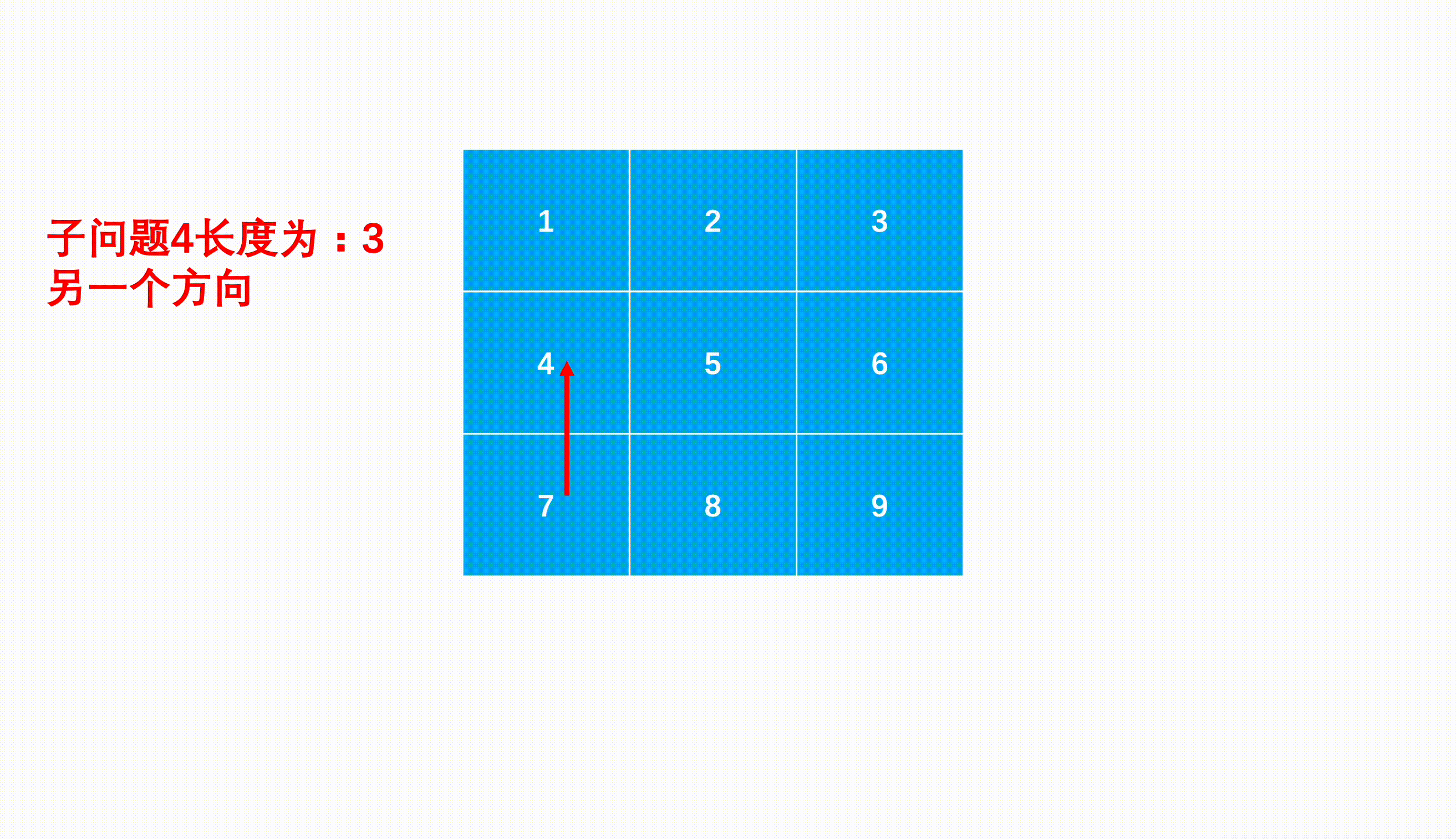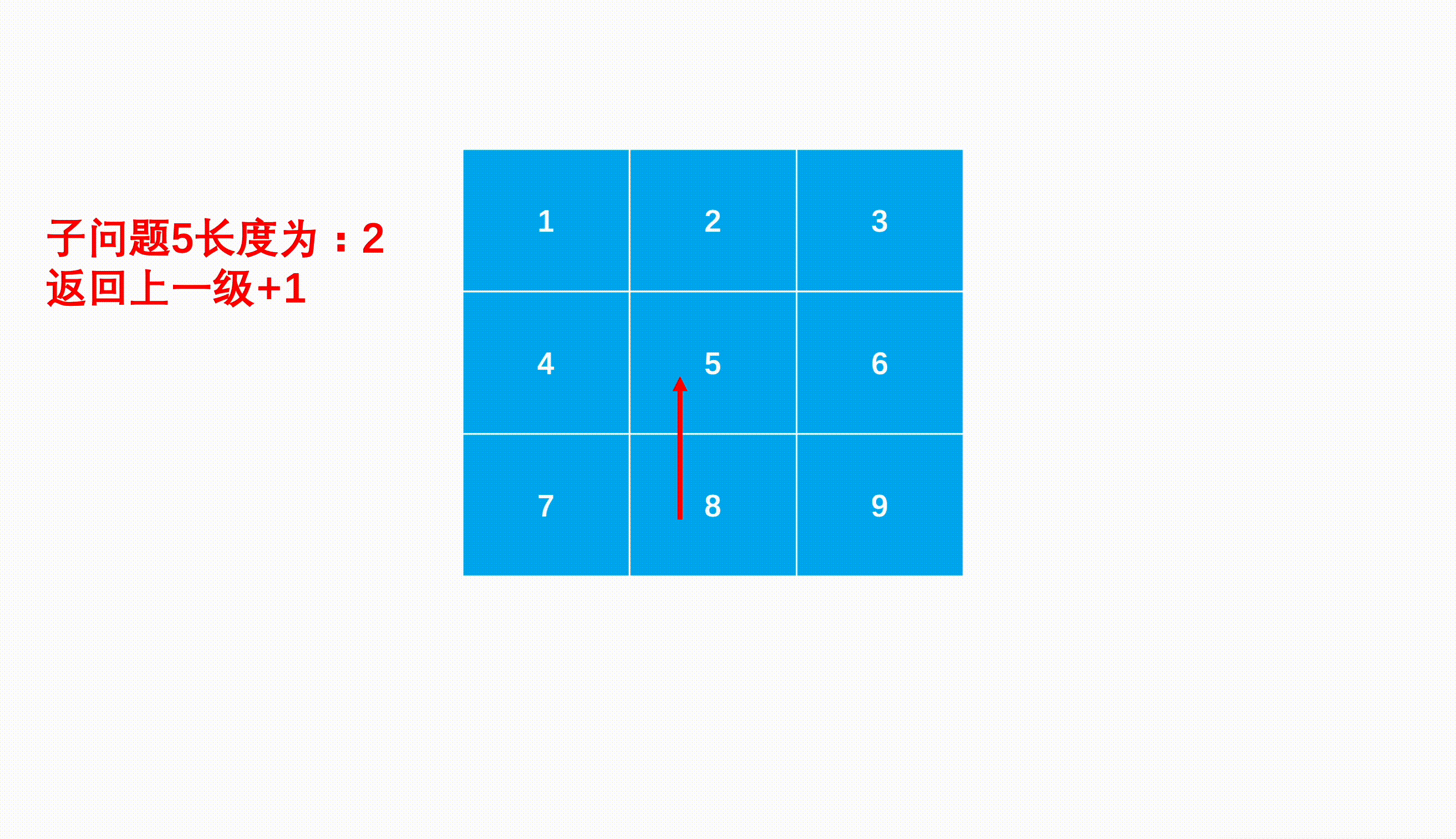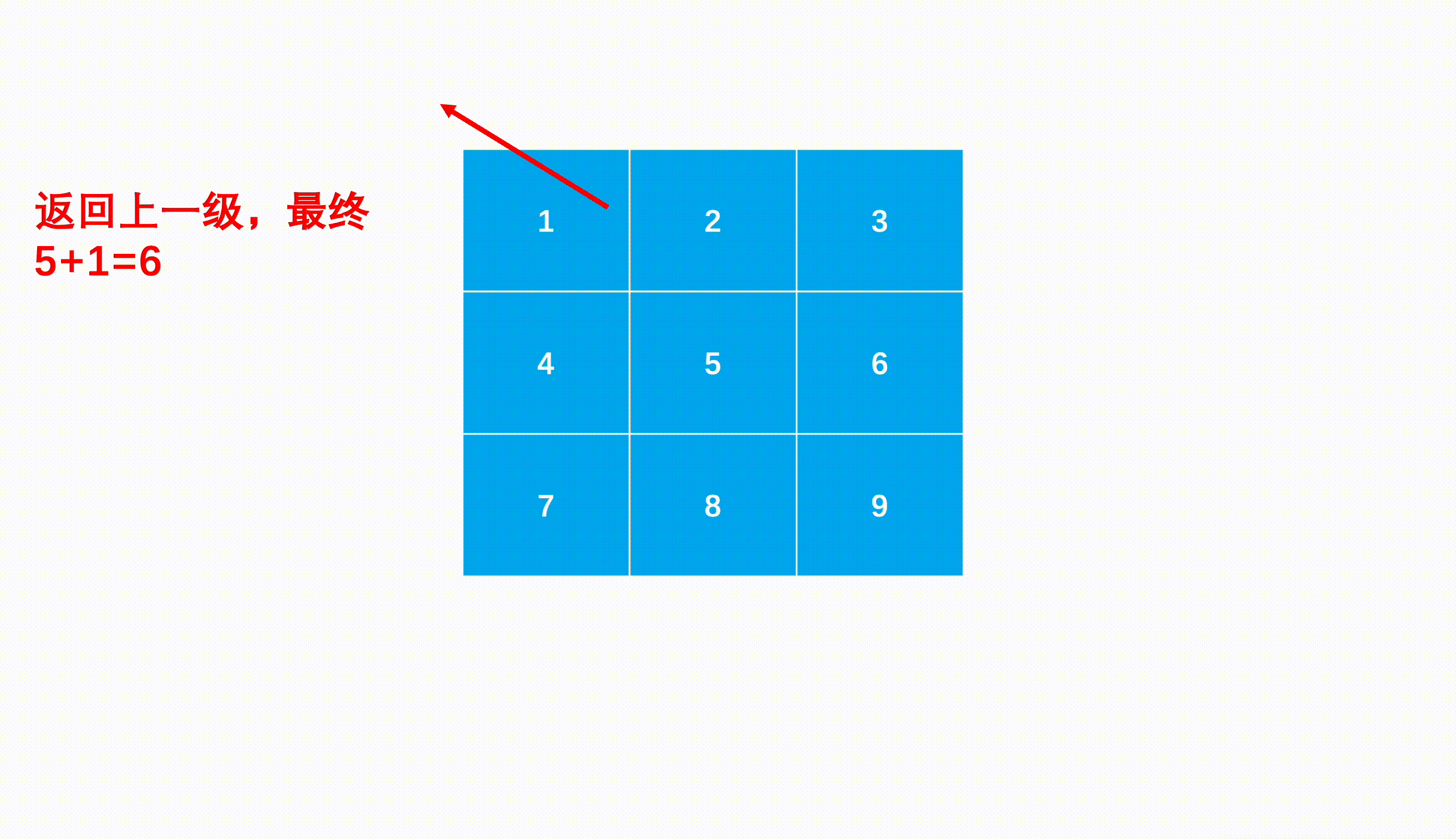
给定一个 n 行 m 列矩阵 matrix ，矩阵内所有数均为非负整数。 你需要在矩阵中找到一条最长路径，使这条路径上的元素是递增的。并输出这条最长路径的长度。

这个路径必须满足以下条件：

1.每个单元格，你可以往上，下，左，右四个方向移动。 你不能在对角线方向上移动或移动到边界外。

2.你不能走重复的单元格。即每个格子最多只能走一次。

思路既然是查找最长的递增路径长度，那我们首先要找到这个路径的起点，起点不好直接找到，就从上到下从左到右遍历矩阵的每个元素。然后以每个元素都可以作为起点查找它能到达的最长递增路径。

如何查找以某个点为起点的最长递增路径呢？我们可以考虑深度优先搜索，因为我们查找递增路径的时候，每次选中路径一个点，然后找到与该点相邻的递增位置，相当于进入这个相邻的点，继续查找递增路径，这就是递归的子问题。因此递归过程如下：

  • 终止条件 进入路径最后一个点后，四个方向要么是矩阵边界，要么没有递增的位置，路径不能再增长，返回上一级。
  • 返回值 每次返回的就是本级之后的子问题中查找到的路径长度加上本级的长度。
  • 本级任务 每次进入一级子问题，先初始化后续路径长度为0，然后遍历四个方向（可以用数组表示，下标对数组元素的加减表示去往四个方向），进入符合不是边界且在递增的邻近位置作为子问题，查找子问题中的递增路径长度。因为有四个方向，所以最多有四种递增路径情况，因此要维护当级子问题的最大值。

具体做法

  1. 使用一个dp数组记录i，j处的单元格拥有的最长递增路径，这样在递归过程中如果访问到就不需要重复访问。
  2. 遍历矩阵每个位置，都可以作为起点，并维护一个最大的路径长度的值。
  3. 对于每个起点，使用dfs查找最长的递增路径：只要下一个位置比当前的位置数字大，就可以深入，同时累加路径长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
//DFS
class Solution {
public:
    int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};	//记录四个方向
    int n, m;
    //深度优先搜索，返回最大单元格数
    
    int dfs(vector<vector<int> > &matrix, vector<vector<int> > &dp, int i, int j) {
        if(dp[i][j] != 0)	return dp[i][j];
        dp[i][j]++;
        for(int k = 0; k < 4; k++){
            int nexti = i + dirs[k][0];
            int nextj = j + dirs[k][1];
            //判断条件
            if (nexti >= 0 && nexti < n && nextj >= 0 && nextj < m && matrix[nexti][nextj] > matrix[i][j]) 
                dp[i][j] = max(dp[i][j], dfs(matrix, dp, nexti, nextj) + 1);
        }
        return dp[i][j];
    }
    
    int solve(vector<vector<int> >& matrix) {
        //矩阵不为空
        if(matrix.size() == 0 || matrix[0].size() == 0) 
            return 0;
        int res = 0;
        n = matrix.size();
        m = matrix[0].size();
        
        //i，j处的单元格拥有的最长递增路径
        vector<vector<int> > dp (n, vector <int> (m));  
        for(int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
                //更新最大值
                res = max(res, dfs(matrix, dp, i, j)); 
        return res;
    }
};

alt

BFS → 有向图的最长路径 → 拓扑排序

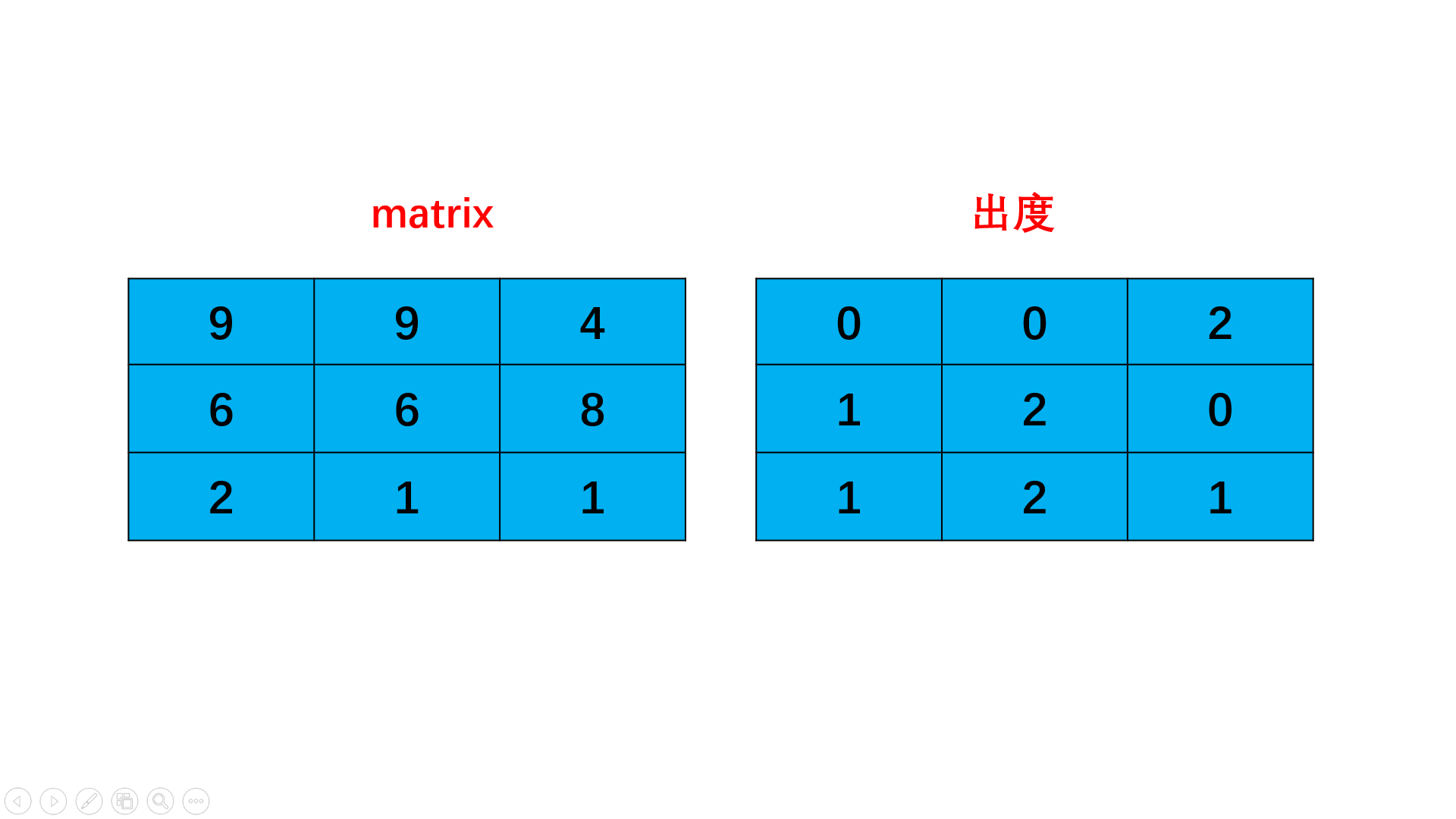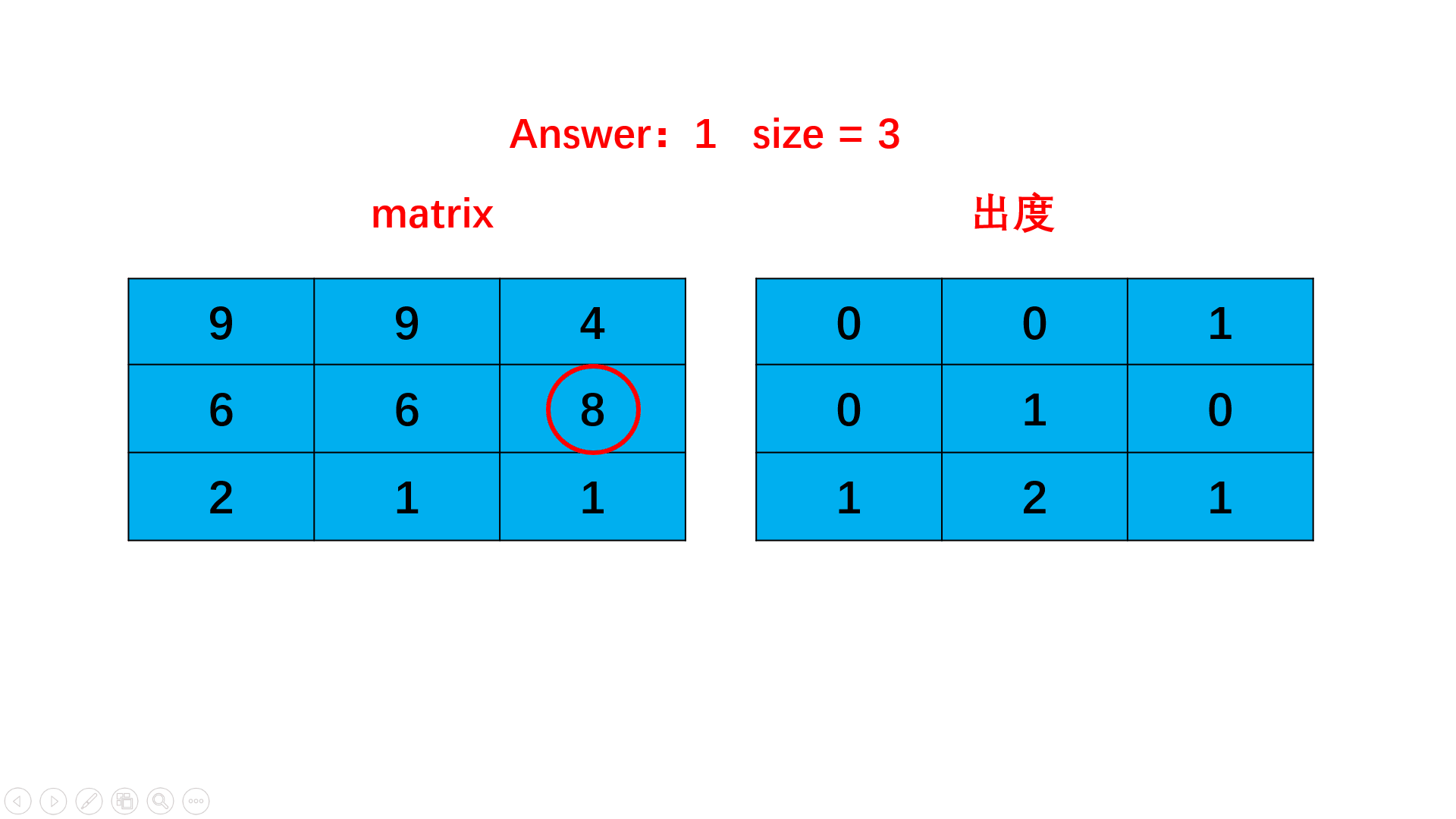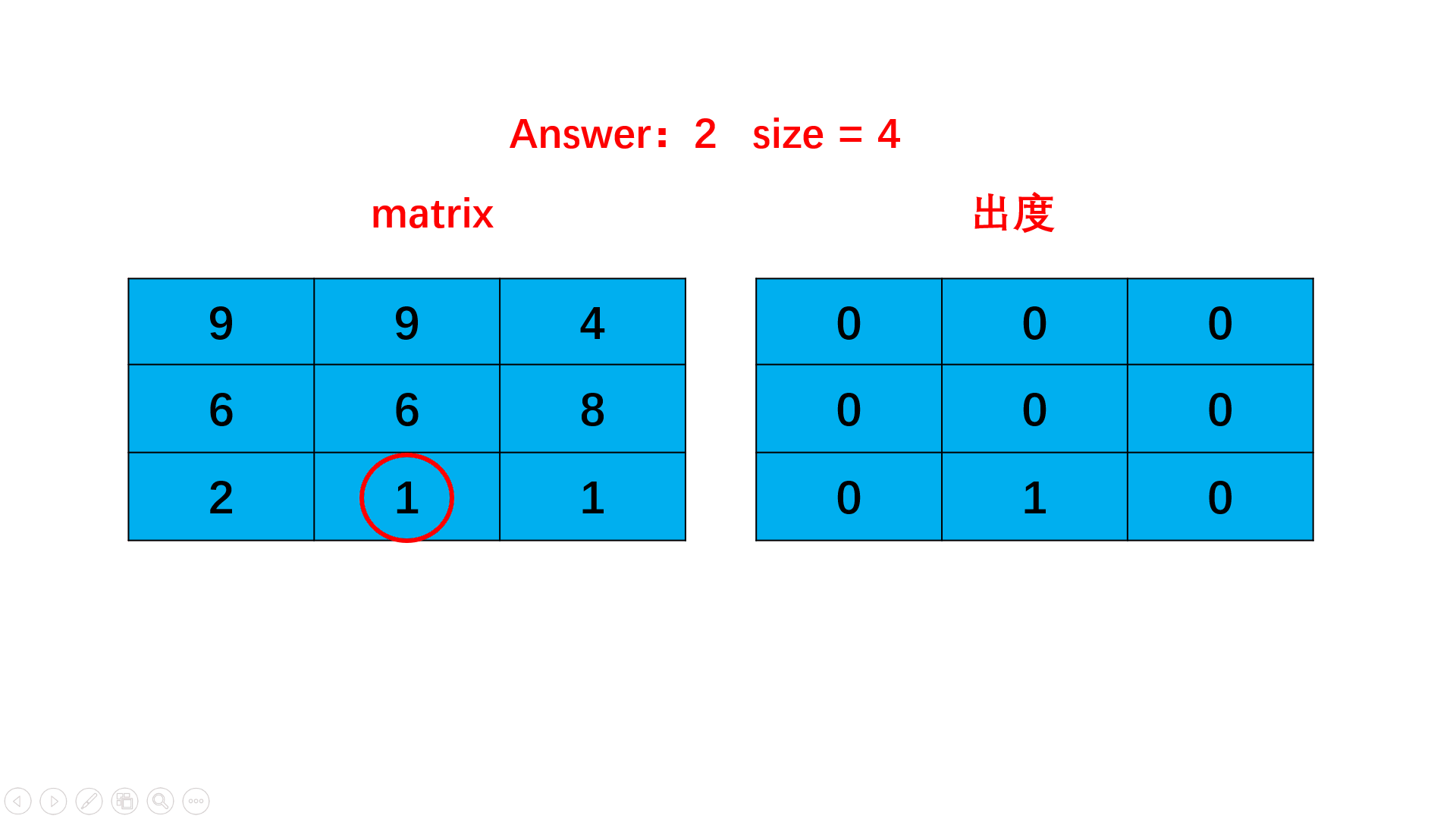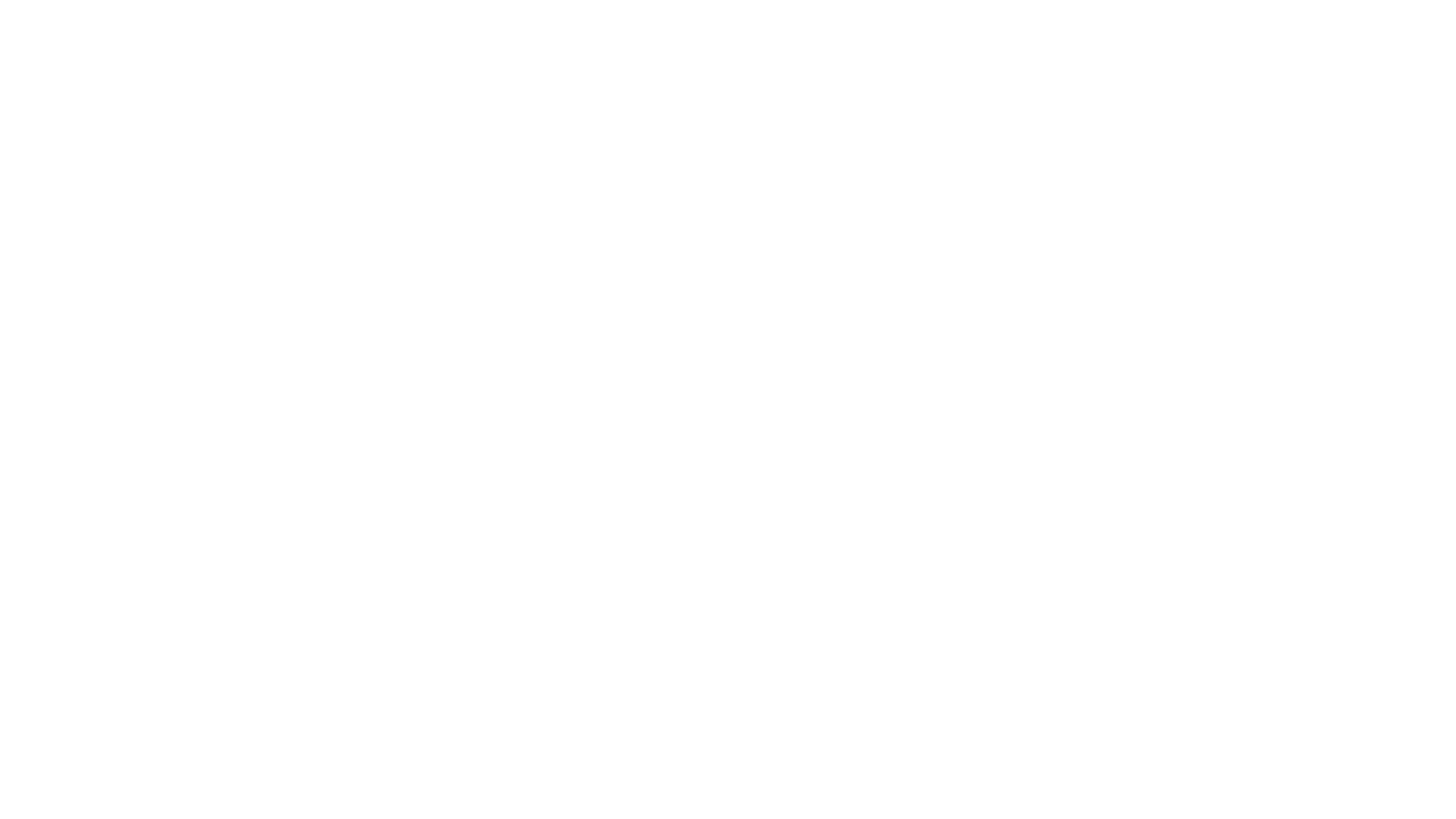
思路将矩阵看成一个有向图，一个元素到另一个元素递增，代表有向图的箭头。这样我们可以根据有向图的出度入度找到最长的路径，且这个路径在矩阵中就是递增的。

具体做法

  1. 计算每个单元格所对应的出度（符合边界条件且递增），作为边界条件的单元格的出度都为0。利用一个二维矩阵记录每个单元格的出度
  2. 利用拓扑排序的思想，从所有出度为0的单元格开始进行广度优先搜索。
  3. 用队列进行bfs，队列中每次加入出度为0的点，即路径最远点，每次从A点到B点，便将A点出度减一。
  4. 每次搜索都会遍历当前层所有单元格，更新其余单元格出度，将出度变为0的单元格加入下一层搜索。
  5. 搜索结束时，搜索的总层数即为矩阵中的最长递增路径的长度，因为bfs的层数就是路径增长的层数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution {
public:
    //记录四个方向
    int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};	//以单元格建立坐标系
    int n, m;
    int solve(vector<vector<int> >& matrix) {
        //空矩阵
        if (matrix.size() == 0 || matrix[0].size() == 0)  
            return 0;
        n = matrix.size();	//行
        m = matrix[0].size();	//列
        
        //记录每个单元的出度
        vector<vector<int> > outdegrees(n, vector<int> (m)); 
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                for (int k = 0; k < 4; k++) {
                    int nexti = i + dirs[k][0];
                    int nextj = j + dirs[k][1];
                    if (nexti >= 0 && nexti < n && nextj >= 0 && nextj < m && matrix[nexti][nextj] > matrix[i][j]) {
                        //符合条件，记录出度
                        outdegrees[i][j]++;
                    }
                }
            }
        }
        
        queue <pair<int, int> > q;
        for (int i = 0; i < n; i++) 
            for (int j = 0; j < m; j++) 
                if (outdegrees[i][j] == 0)
                    //找到出度为0的入队列
                    q.push({i, j});
        
        int res = 0;
        while (!q.empty()) {
            res++;
            int size = q.size();
            for (int x = 0; x < size; x++) {
                pair<int, int> temp = q.front(); 
                q.pop();
                int i = temp.first;
                int j = temp.second;
                //四个方向
                for (int k = 0; k < 4; k++) { 
                    int nexti = i + dirs[k][0];
                    int nextj = j + dirs[k][1];
                    //逆向搜索，所以下一步是小于
                    if (nexti >= 0 && nexti < n && nextj >= 0 && nextj < m && matrix[nexti][nextj] < matrix[i][j]) {
                        //符合条件，出度递减
                        outdegrees[nexti][nextj]--; 
                        if (outdegrees[nexti][nextj] == 0) {
                            q.push({nexti, nextj});
                        }
                    }
                }
            }
        }
        return res;
    }
};

图片说明

动态规划

BM62 斐波那契数列

描述 斐波那契数列，输入一个正整数 n ，输出斐波那契数列的第 n 项。

$$fib(x)= \begin{cases} 1& \text{x=0,2}\ fib(x-1)+fib(x-2)& \text{x>2} \end{cases}$$

要求：空间复杂度 O(1)，时间复杂度 O(n)，本题也有时间复杂度 O(logn)的解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
//递归算法
class Solution {
public:
    int Fibonacci(int n) {
        if(n <= 2)	return 1;
        else
            return Fibonacci(n - 1) + Fibonacci(n - 2);
    }
};

//记忆化搜索
class Solution {
public:
    int f[50]{0};
    int Fibonacci(int n) {
        if (n <= 2)	     return 1;
        if (f[n] > 0)	return f[n];
        return f[n] = (Fibonacci(n-1)+Fibonacci(n-2));
    }
};

//动态规划1
class Solution {
public:
    int dp[50]{0};
    int Fibonacci(int n) {
        dp[1] = 1, dp[2] =1;
        for (int i = 3 ; i <= n ; i ++) dp[i] = dp[i-1]+dp[i-2];
        return dp[n];
    }
};

//动态规划2
class Solution {
public:
    int Fibonacci(int n) {
        int a = 1 , b = 1 , c = 1;
        for (int i = 3 ; i <= n ; i ++) {
            c = a+b , a = b , b = c;
        }
        return c;
    }
};

BM63 跳台阶

描述 同斐波那契数列

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

要求：时间复杂度：O(n)，空间复杂度： O(1)

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int jumpFloor(int number) {
        int a = 1 , b = 1 , c = 1;
        for (int i = 2 ; i <= number ; i ++) {
            c = a+b , a = b , b = c;
        }
        return c;
    }
};

BM64 最小花费爬楼梯

描述 给定一个整数数组 cost，其中 cost[i]是从楼梯第i个台阶向上爬需要支付的费用，下标从0开始。

一旦你支付此费用，即可选择向上爬一个或者两个台阶。你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。请你计算并返回达到楼梯顶部的最低花费。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        //dp[i]表示爬到第i阶楼梯需要的最小花费
        vector<int> dp(cost.size() + 1, 0); 
        for(int i = 2; i <= cost.size(); i++)
            //每次选取最小的方案
            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]); 
        return dp[cost.size()];
    }
};

BM65 最长公共子序列

描述 给定两个字符串str1和str2，输出两个字符串的最长公共子序列。如果最长公共子序列为空，则返回”-1”。目前给出的数据，仅仅会存在一个最长的公共子序列

输入：”1A2C3D4B56”,”B1D23A456A”

输出：”123456”

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    string LCS(string s1, string s2) {
        if(s1.empty() || s2.empty()) return "-1";
        int dp[s1.size()+1][s2.size()+1];
        for(int i = 0; i <= s1.size(); i++) 
            dp[i][0] = 0;
        for(int j = 0; j <= s2.size(); j++) 
            dp[0][j] = 0;
        for(int i = 1; i <= s1.size(); i++) {
            for(int j = 1; j <= s2.size(); j++) 
                dp[i][j] = (s1[i-1] == s2[j-1]) ? dp[i-1][j-1] + 1: max(dp[i-1][j], dp[i][j-1]); 
        }
        string res = "";
        for(int i = s1.size(), j = s2.size(); dp[i][j] >= 1;) {
            if(s1[i-1] == s2[j-1]) {
                res += s1[i-1];
                i--;j--;
            }
            else if(dp[i-1][j] >= dp[i][j-1]) i--;
            else j--;
        }
        reverse(res.begin(), res.end());
        return res.empty() ? "-1" : res;
    }
};

BM66 最长公共子串

给定两个字符串str1和str2,输出两个字符串的最长公共子串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    string LCS(string str1, string str2) {
        //dp[i][j]表示到str1第i个个到str2第j个为止的公共子串长度
        vector<vector<int> > dp(str1.length() + 1, vector<int>(str2.length() + 1, 0)); 
        int max = 0;
        int pos = 0;
        for(int i = 1; i <= str1.length(); i++){
            for(int j = 1; j <= str2.length(); j++){
                //如果该两位相同
                if(str1[i - 1] == str2[j - 1]){ 
                    //则增加长度
                    dp[i][j] = dp[i - 1][j - 1] + 1; 
                }
                else{ 
                    //该位置为0
                    dp[i][j] = 0; 
                }
                //更新最大长度
                if(dp[i][j] > max){ 
                    max = dp[i][j];
                    pos = i - 1;
                }
            }
        }
        return str1.substr(pos - max + 1, max);
    }
};

BM67 不同路径的数目(一)

一个机器人在m×n大小的地图的左上角（起点）。

机器人每次可以向下或向右移动。机器人要到达地图的右下角（终点）。

可以有多少种不同的路径从起点走到终点？

起点
终点

要求：空间复杂度 O(nm)，时间复杂度 O(nm)

进阶：空间复杂度 O(1)，时间复杂度 O(min(n,m))

34

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int uniquePaths(int m, int n) {
       vector<vector<int>>dp(m,vector<int>(n,0));
       //第一行初始化，只有一条路径
       for(int i=0;i<n;i++){
           dp[0][i] = 1;
       }
       //第一列初始化，只有一条路径
       for(int i=0;i<m;i++){
           dp[i][0] =1;
       }
       for(int i=1;i<m;i++){
           for(int j=1;j<n;j++){
               //转移方程
               dp[i][j] = dp[i-1][j]+dp[i][j-1];
           }
       }
       return dp[m-1][n-1];
1
2
3
4
5
6
7
8
9
 //数学求解
    int uniquePaths(int m, int n) {
    long long ret = 1;
    for (int x = n, y = 1; y < m; ++x, ++y) {
        //组合公式的循环求解
        ret = ret * x / y;
    }
    return ret;
}

BM68 矩阵的最小路径和

描述 给定一个 n * m 的矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。

要求：时间复杂度 O(nm)

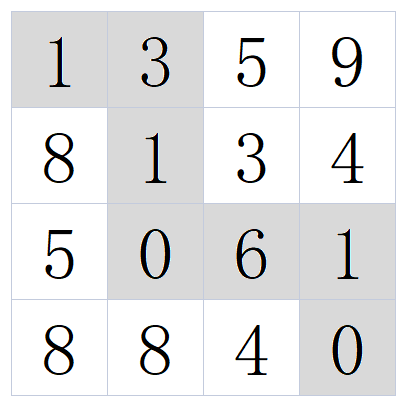
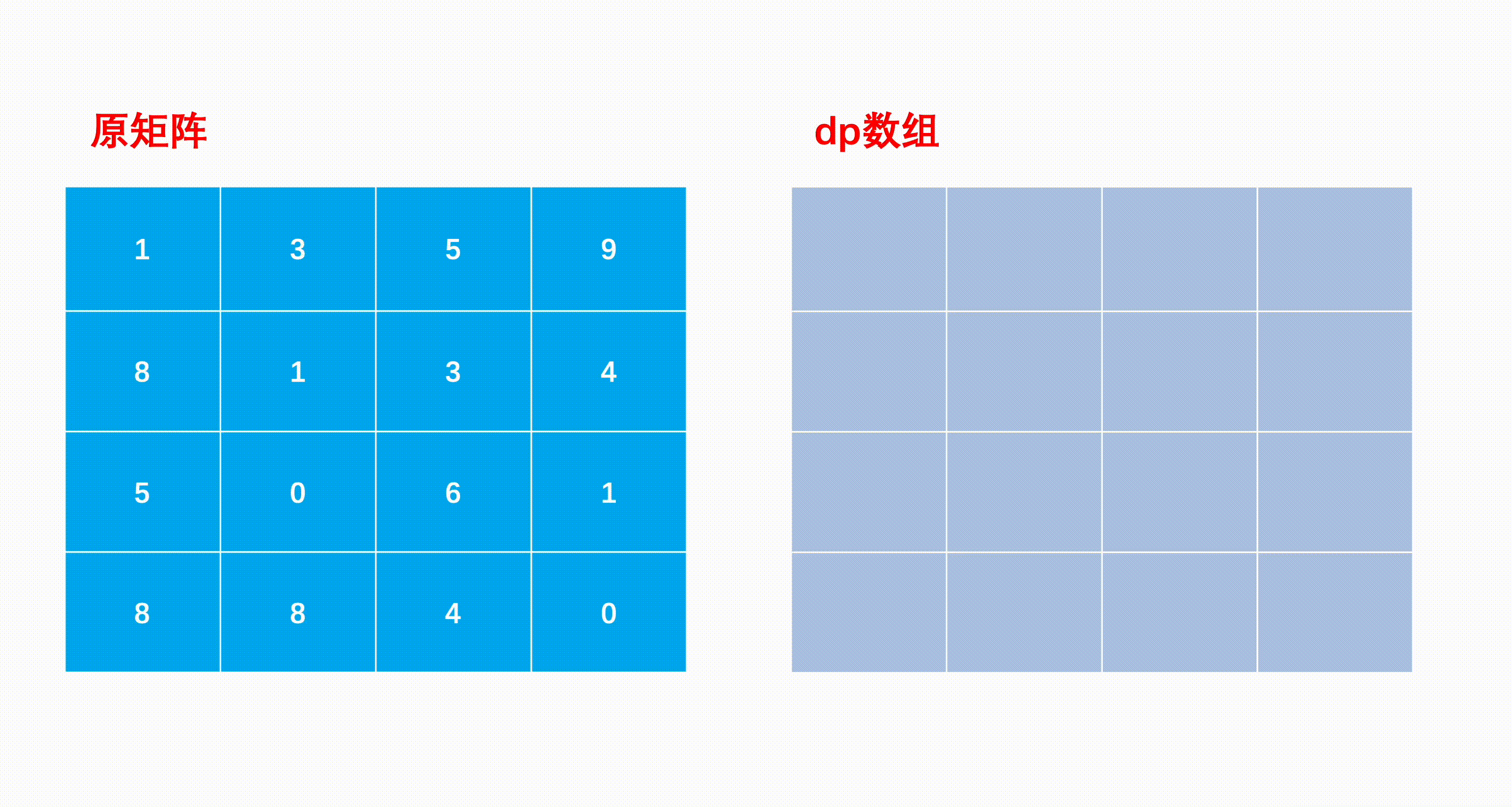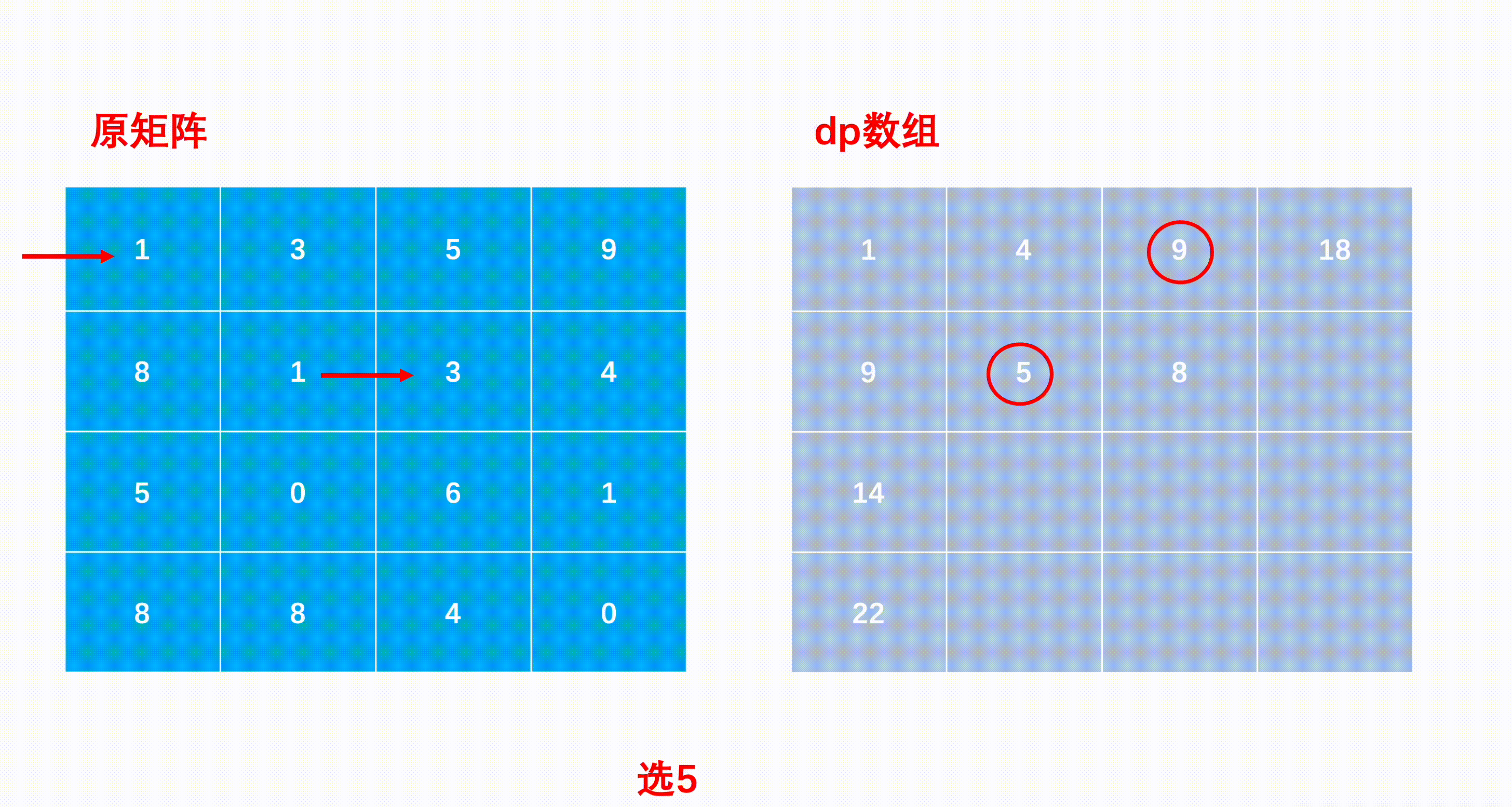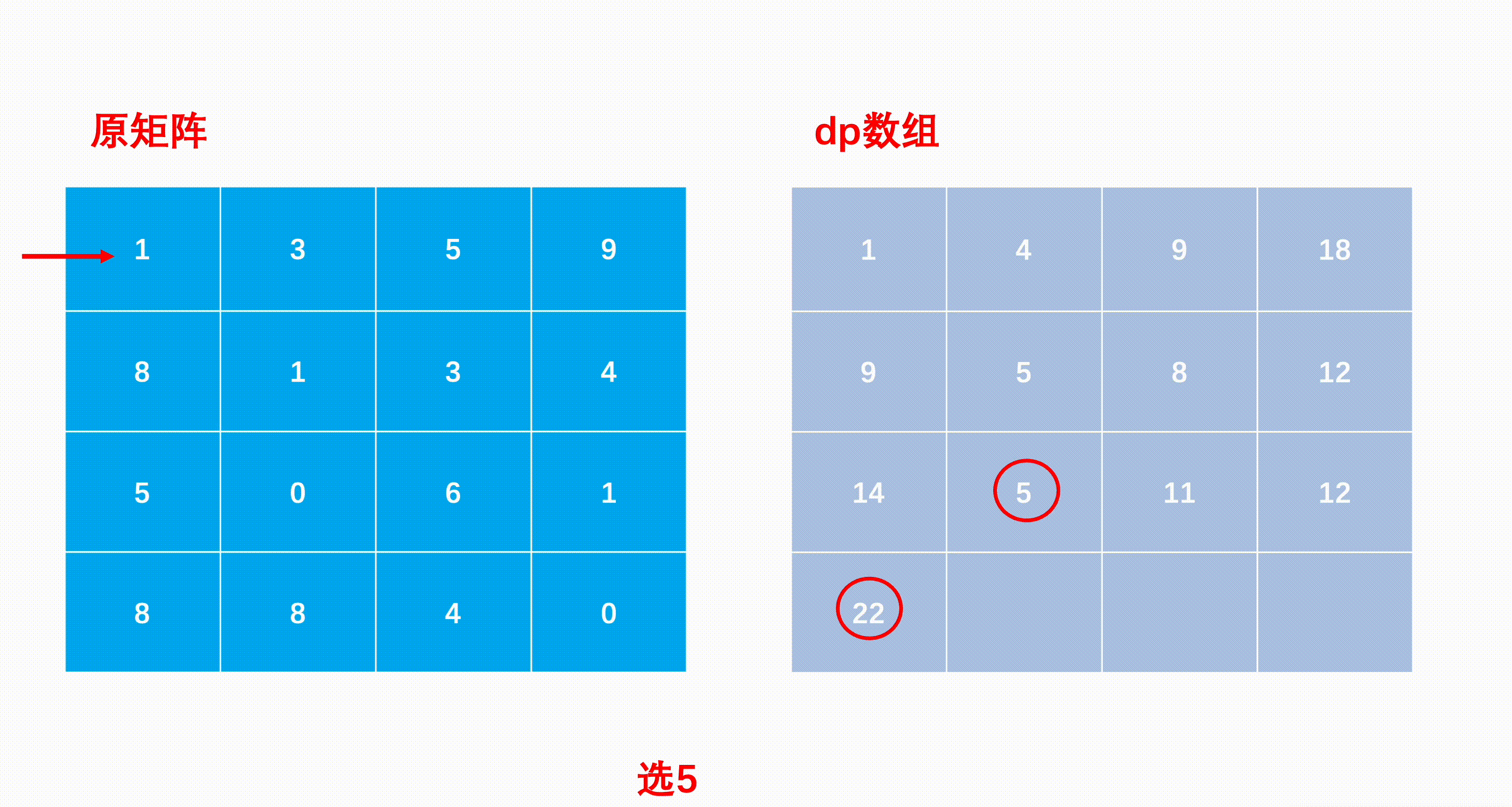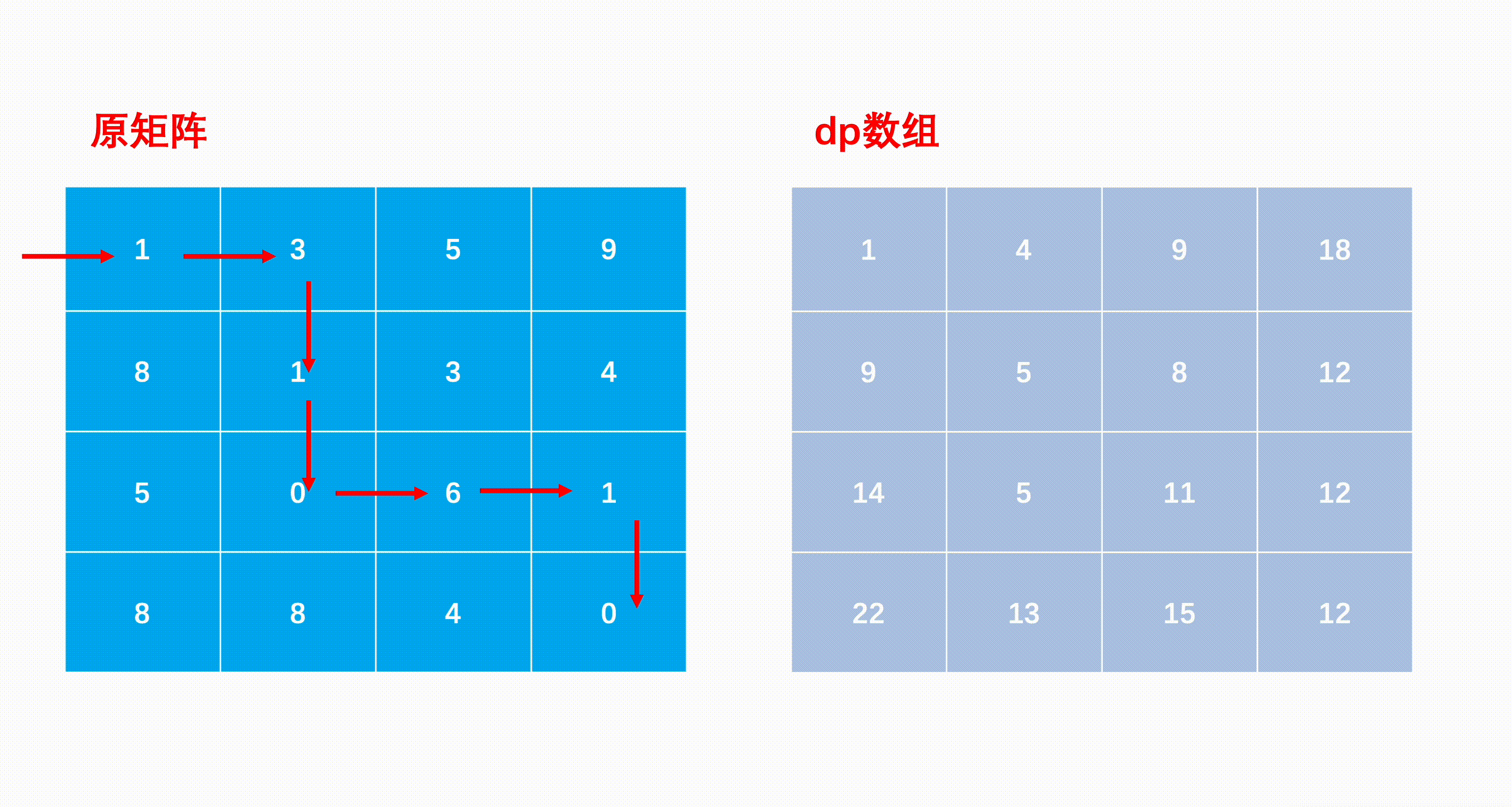
例如：当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时，对应的返回值为12，

所选择的最小累加和路径如下图所示：

imgalt

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int minPathSum(vector<vector<int> >& matrix) {
        int n = matrix.size();
        int m = matrix[0].size();  
        //dp[i][j]表示以当前i，j位置为终点的最短路径长度
        vector<vector<int> > dp(n + 1, vector<int>(m + 1, 0));
        dp[0][0] = matrix[0][0];
        //处理第一列
        for(int i = 1; i < n; i++)
            dp[i][0] = matrix[i][0] + dp[i - 1][0];
        //处理第一行
        for(int j = 1; j < m; j++)
            dp[0][j] = matrix[0][j] + dp[0][j - 1];
        //其他按照公式来
        for(int i = 1; i < n; i++){ 
          for(int j = 1; j < m; j++){
              dp[i][j] = matrix[i][j] + (dp[i - 1][j] > dp[i][j - 1] ? dp[i][j - 1] : dp[i - 1][j]);
          }
      }
       return dp[n - 1][m - 1];
    }
};

少先队长Software Engineer

第四公民